Find the value of x for which \begin{equation} e^x-1= 2x \end{equation} Some numerical or analytical methods are appreciated, thanks.
Using graphic inspection, we have that
We can observe that there are two solutions: $x=0$ and,approximately, $x=1.25643...$
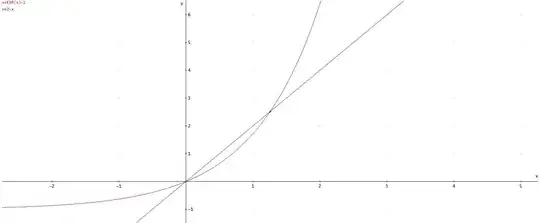
By hand
Plot the points $(0,1)$, $(1,e\approx2.7)$, $(2,e^2\approx 7.3)$ on the exponential and intercept with $2x+1$.
Visually,$$x\approx1.3.$$
Using a four operations calculator
Use a Talyor's development to the second order from $x=1$. $$e^x-1=ee^{x-1}-1\approx e(1+(x-1)+(x-1)^2/2)-1=2x,$$ $$ex^2-4x+e-2=0,$$ $$x\approx\frac{2+\sqrt{4-e(e-2)}}e=1.262$$
Using a simple scientific calculator
Repeat the sequence of keypress [*][2][+][1][=][Ln] until convergence (30 times or so), starting from an approximation like 1.262.
This performs the fixed-point iteration $x_{n+1}=\ln(2x_n+1)$, which gives the solution.
$$x\approx1.25643121.$$
Analytically
Consider the function $y(x)=e^x-2x-1$, its inverse $x(y)$, and the Taylor development of the latter: $$\frac{dx}{dy}=\frac1{\frac{dy}{dx}}=\frac1{e^x-2},$$ then by the chain rule, $$\frac{d^2x}{dy^2}=-\frac{e^x}{(e^x-2)^2}\frac{dx}{dy}=-\frac{e^x}{(e^x-2)^3},$$ $$\frac{d^3x}{dy^3}=\Big(-\frac{e^x}{(e^x-2)^3}+\frac{3e^{2x}}{(e^x-2)^4}\Big)\frac{dx}{dy}=-\frac{e^x}{(e^x-2)^4}+\frac{3e^{2x}}{(e^x-2)^5},$$ $$...$$ You can develop around a close approximation of the root, $x_0=\frac54, y_0=e^{x_0}-2x_0-1$, giving $$x(y)=x_0+\frac1{e^{x_0}-2}(y-y_0)-\frac{e^{x_0}}{(e^{x_0}-2)^3}\frac12(y-y_0)^2+\\\Big(-\frac{e^{x_0}}{(e^{x_0}-2)^4}+\frac{3e^{2{x_0}}}{(e^{x_0}-2)^5}\Big)\frac16(y-y_0)^3+...$$ Then evaluate $$x(0)=x_0-\frac1{e^{x_0}-2}y_0-\frac{e^{x_0}}{(e^{x_0}-2)^3}\frac12y_0^2-\\\Big(-\frac{e^{x_0}}{(e^{x_0}-2)^4}+\frac{3e^{2{x_0}}}{(e^{x_0}-2)^5}\Big)\frac16y_0^3+...\\\approx1.25 + 0.00647974514175 - 4.91663237447\cdot10^{-5} - 6.39922963124\cdot10^{-7}-1.02964389462\cdot10^{-8}=1.2564299286$$
As T. Bongers commented, beside the trivial root $x=0$, there is one root which can be made explicit using Lambert function. It is given by $$x=-W_{-1}\left(-\frac{1}{2 \sqrt{e}}\right)-\frac{1}{2}$$ Its numerical value has been given by JimmyK4542.
Please notice that any equation of the form $A+B x+ C \log(D + E x)=0$ has solutions which, it they exist, can be expressed using Lambert function.
If you are looking for a numerical method for solving $$f(x)=e^x-1-2x=0$$ consider one of the simplest which is Newton (which exhibits a quadratic convergence); starting with a "reasonable" guess of the solution $x_0$, Newton scheme will update it according to $$x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)}$$ As JimmyK4542 showed, there is a solution between $1$ and $2$. So, let us choose $x_0=1$. The above scheme will then provide the following iterates : $1.39221$, $1.27396$, $1.25678$, $1.25643$ which is the solution for six significant figures.
Being slightly less lazy, and knowing that the solution is between $1$ and $2$, we could have expand $f(x)$ as a first order McLaurin series built at $x=\frac{3}{2}$; this gives $$f(x)=\left(e^{3/2}-4\right)+\left(e^{3/2}-2\right) \left(x-\frac{3}{2}\right)+O\left(\left(x-\frac{3}{2}\right)^2\right)$$ which would give $$x=\frac{2+e^{3/2}}{2 \left(e^{3/2}-2\right)}\simeq 1.30590$$ and start Newton iteration from this value.
Use Lambert's W function. The general equation: $$ ~p^{a x + b} = c x + d $$
is solved in the examples of the corresponding Wiki page: $$ x = -\frac{W(-\frac{a\ln p}{c}\,p^{b-\frac{a d}{c}})}{a\ln p} - \frac{d}{c} $$ Wolfram|Alpha can also help...
Let $f(x) = e^x-2x-1$. Then, $f'(x) = e^x-2$ and $f''(x) = e^x > 0$.
Therefore, $f(x)$ is concave up, and thus, $f(x)$ can have at most two roots.
Clearly, $f(0) = 0$, so $x = 0$ is a solution.
Since $f(1) = e-3 < 0 < e^2-5 = f(2)$, the other root is somewhere between $1$ and $2$.
This root will need you to use numerical methods. I'm getting $x \approx 1.256431$ for the other root.
If $e^x-1=2x$, then we can use the Lambert W function: $$ \begin{align} e^x-2x&=1\\ e^{-2x}e^{e^x}&=e\\ e^xe^{-\frac12\large e^x}&=e^{-\frac12}\\ -\tfrac12e^xe^{-\frac12\large e^x}&=-\tfrac12e^{-\frac12}\\ -\tfrac12e^x&=\mathrm{W}\left(-\tfrac12e^{-\frac12}\right)\\ x&=\log\left(-2\mathrm{W}\left(-\tfrac12e^{-\frac12}\right)\right) \end{align} $$ Now, of course, one branch gives $\mathrm{W}\left(-\frac12e^{-\frac12}\right)=-\frac12$, which yields $$ x=0 $$ However, for values of its argument in $\left[-\frac1e,0\right)$, Lambert W has two real branches, and the other branch gives $\mathrm{W}\left(-\frac12e^{-\frac12}\right)=-1.7564312086261696770$, which yields $$ x=1.2564312086261696770 $$
In this answer, I develop an iterative method for computing Lambert W.
For $t=-\frac12e^{-\frac12}=-0.303265329856317$, it proceeds as follows:
Initial guess for the non-principal value: $t\lt-0.1$, so we use an initial $w_0=-2$.
Now we iterate
$$
w_{n+1}=\frac{te^{-w_n}+w_n^2}{w_n+1}
$$
$$
\begin{array}{l}
w_0=-2\\
w_1=-1.75915546483097\\
w_2=-1.75643239139964\\
w_3=-1.75643120862639\\
w_4=-1.75643120862617\\
w_5=-1.75643120862617
\end{array}
$$
So $x=\log(-2\times-1.75643120862617)=1.25643120862617$
