38

In watching The Fault in Our Stars I could not help but cringe at a line that flew in the face of mathematics and subsequently ruined the movie for me:

"There are infinite numbers between 0 and 1. There's .1 and .12 and .112 and an infinite collection of others. Of course, there is a bigger infinite set of numbers between 0 and 2, or between 0 and a million. Some infinities are bigger than other infinities." - John Green

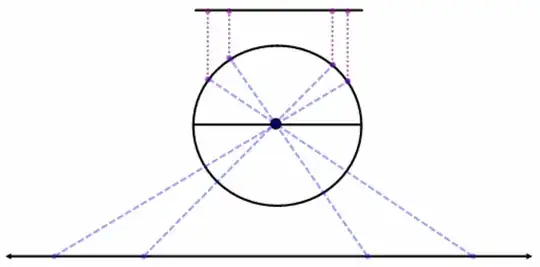
While walking out of the theater I tried to explain to my friends why there were, in fact, exactly the same amount of numbers between 0 and 1 as 0 and 2, but Cantor and bijective functions are not great learning tools to English majors.

Does anybody have an eloquent or elegant way to enumerate this phenomenon using an example accessible to those not familiar with advanced mathematics?

user151675
  • 423
  • 22
    Just tell them "If you didn't know how to count a set of three sheep and a set of three shoes, how would you know they are just as many sheep as shoes?" They would intuitively respond that you can pair each sheep with exactly one shoe. Then tell them you can do the same thing with the numbers between 0 and 1 and the numbers between 0 and 2, but that it requires some math to pair them up in such a way -- however, the concept is still the same because they can be paired up. – layman Jul 14 '14 at 18:00
  • This is above my understanding, but... it seems that there should be more between 0 and 2? From my sense. – Rivasa Jul 14 '14 at 18:00
  • 3
    @Link: It goes against your intuition because in mathematics, as one extends counting to infinite sets, the concept dissociates from that of inclusion. So while, the set of numbers between 0 and 1 is contained within the set of numbers between 0 and 2, each member of the former set can be matched with its double in the latter set, hence there is an equal amount of numbers in both. This cannot happen with finite sets which is what your intuition is built upon. – Raskolnikov Jul 14 '14 at 18:03
  • 2
    Not only do $(0,1)$ and $(0,2)$ have the same cardinality, but in fact, they have the same order-type. So John really messed that one up. – goblin GONE Jul 14 '14 at 18:05
  • @Raskolnikov what you mean by "double" I mean, to me say, 0.1111.. and 1.1111... they seem to be inherently different numbers? – Rivasa Jul 14 '14 at 18:06
  • 1
    Here's a fun video that tries to explain this for people with a lesser background in math. https://www.youtube.com/watch?v=UPA3bwVVzGI – layman Jul 14 '14 at 18:07
  • 2
    @Link: $0.2=2 \times 0.1$ – Raskolnikov Jul 14 '14 at 21:05
  • 31
    The author stated it was intentional on his part. "The idea there was that I liked that 16-year-olds could make—as they do—incorrect abstract conclusions about complex mathematics. But even if these conclusions are incorrect, they can provide real and lasting consolation. I felt like it would be too neat/tidy to have everything be correct; I wanted her to make incorrect inferences from Van Houten’s monologue that still guide her thinking in a correct/helpful direction." – Ryan Jul 14 '14 at 22:04
  • You are also wrong, because you used the word "amount" to describe what is between 0 and 1. If you approach it that way, you will lose to the English majors: rightfully so. – Kaz Jul 15 '14 at 03:18
  • "... The vault is not on our stairs, but on our shelves." – keshlam Jul 15 '14 at 06:45
  • 2
    @Raskolnikov It doesn't really mean anything to say that there are the same "amount" of numbers in both. Note that the two sets have different measures. All we can say is that they have the same cardinality, which means nothing more or less than that their elements can be put in bijective correspondence. –  Jul 15 '14 at 19:03

8 Answers8

44

Look, don't worry about it. The author is absolutely correct if by "bigger" he means bigger Lebesgue measure rather than bigger cardinality. Cardinality is just one way to abstract our intuitions about size and it isn't obviously the best one to use in all situations (especially in this kind of situation where it returns highly counterintuitive results).

Qiaochu Yuan
  • 419,620
  • 20
    I agree with the "don't worry about it" part since they're English majors and it won't hurt them to believe an incorrect statement or two about infinite sets, but I think the wording of the quote clearly rules out a Lebesgue-measure interpretation. After all, it talks about the number of points between $0$ and $1$, and explicitly states that there are infinitely many such points; but the length $(0,1)$ is emphatically finite. – goblin GONE Jul 14 '14 at 18:14
  • As @user18921 pointed out, it's clear the author is talking about a more "set oriented" concept of "size". He doesn't explicitly state that he's using cardinality, but it's clear he's not talking about Lebesgue measure. However, he could easily be implicitly talking about ordering sets by inclusion. – Jack M Jul 14 '14 at 18:30
  • 2
    Also, the author says he wants to compare infinities, not subsets of $\mathbb R$ – Hagen von Eitzen Jul 14 '14 at 18:32
  • 1
    Also, the author has a scientifically-minded brother and a very geeky audience, both of whom should have put him right on this. – TRiG Jul 14 '14 at 20:46
  • 6
    See my comment at the original question. It was an intentional error by the author. – Ryan Jul 14 '14 at 22:06
  • 9
    "Look, don't worry about it" = words to live by – Ben Millwood Jul 14 '14 at 22:10
34

Assume Alice has a basket with balls in it, one for each real number between $0$ and $1$, which is written on the ball. OK, it is hard to imagine so many balls - or even how one would manage to write down an arbitrary real number on such a ball, but that is not the point here.

Bob also has such a basket, also with one ball for each real number between $0$ and $1$. If there is any concept to make sense of this at all, we can only say that Alice and Bob have the same number of balls in the basket.

What if Bob took out his marker pen and painted a green dot on each of his balls? Of course, the two buddies still have the same number of balls.

What if Bob instead would prepend the symbols "$2\times$" before the number written on the ball? Of course, the two buddies still have the same number of balls. The difference to the previous example is minor - green dot or a digit and a times symbol, that does not make a difference.

What if Bob now for each of his balls replaces the number ($x$, say) written on it with the number $2x$? Of ocurse they still have the same number of balls. The difference to the provious example is minor - whether the ball has "$2\times0.314159$" written on it or "$0.628318$" doesn't matter.

Now on closer look, Bob notices that in his basket he has one ball for each real number between $0$ and $2$.

We conclude that there are just as many numbers between $0$ and $1$ as there are between $0$ and $2$.

Jens Björnhager
  • 103
Hagen von Eitzen
  • 374,180
  • The English phrase "as many" implies counting. But the infinity is not countable, so this phrase does not apply in the sense of not connecting with that concept. You cannot put a segment of the real number line in a 1:1 correspondence with golf balls. – Kaz Jul 15 '14 at 03:24
  • @Kaz Yes I can, I just cannot place these in a bag in physical space with each ball having positive volume. But one gets similar problems already with countably many balls. I used this anecdote to literally tear apart the real numbers, depriving them of any disturbing properties (such as their topology). – Hagen von Eitzen Jul 16 '14 at 15:29
14

Draw two parallel line segments, a small one and a big one, then construct the triangle formed by uniting their end-points. Notice now how to each line determined by the newly-obtained vertex and a point on the small segment there corresponds exactly one point on the bigger segment, and vice-versa, thus proving that the two have the exact same number of points, regardless of their different lengths.

Lucian
  • 48,334
  • 2
  • 83
  • 154
  • I think this is the simplest way. Compare sets by matching elements, and see that there are none left. – Davidmh Jul 15 '14 at 09:40
  • Not only is it the simplest, it also teaches people how to think in proper terms when it comes to set theory. – jpmc26 Jul 15 '14 at 22:40
  • How does one form a triangle when uniting the end points of two parallel lines? Doesn't a triangle have 3 points and don't two parallel lines have four points? – CramerTV Jul 16 '14 at 16:52
  • @CramerTV: Would this answer your question ? – Lucian Jul 16 '14 at 23:42
  • @Lucian, Perfect, yes, thank you - think outside the box as it were. But it raises another question in my mind. If we are using this triangle to show that any two line segments have the same number of points, if taken to the extreme then the single point at the vertex would have the same number of points as the longest line segment :/ I do grasp the concept of Cantor's diagonal argument though, where an infinite set does not contain all of the numbers. I believe though, that infinity is simply a useful 'construct' and we should just stop talking about it as though it is an actual number. – CramerTV Jul 17 '14 at 16:42
  • @CramerTV: As I said, for each point situated on one segment we have exactly one corresponding point on the other segment, and vice-versa. But the one point at the top cannot be said to be different from itself. – Lucian Jul 17 '14 at 22:43
  • While I knew the 'point is not a line' was the logical argument against my 'extreme' example, telling someone that the line of (two) points infinitesimally close to the vertex has the same number of points as one infinitely far away from that vertex still stretches credulity in my mind. I am not well versed in set theory so take my comments in that context. I saw this question and just wanted to learn more - and I did by reading a bit in wikipedia about Cantor sets and bijective functions. Although every time I hear Cantor in my mind I am reminded of Eric Cantor. ;) – CramerTV Jul 18 '14 at 00:31
  • 1
    @CramerTV: Perhaps it does stretch credulity. But the geometric construction is merely an embodiment of the more abstract theory. If someone disbelieves even something they can touch and see, how much more so something they can't? Another way is to take, for instance, $f(x)=\dfrac1x$, which creates a bijection between $[0,1]$ and $[1,\infty]$. – Lucian Jul 18 '14 at 00:48
  • Thank you - that simple example fixed the concept for me. I can see that any number x maps to a value in the other set with just a couple of concrete examples. I am not an English major but I suspect this simple example is easily accessible by most folks. – CramerTV Jul 18 '14 at 00:59
2

If you drive $60$ kilometers per hour you will traverse one kilometer in one minute. If you drive $120$ kilometers per hour you will traverse two kilometers in one minute. In this way each distance in between $0$ and $1$ kilometer correspond to a time in between $0$ and $1$ minute. But, the same is true for each distance between $0$ and $2$ kilometers.

J126
  • 17,451
1

Think of a group of girls, and a group of boys. Which group is bigger? We can match them up in pairs to see. If we have one boy for every girl and vice versa, then the number of girls is the same as boys.

So it is with the numbers. Take any number in between 0 and 1, and multiply it by 2. That gives a number between 0 and 2, so we have paired up numbers between 0 and 1 with numbers between 0 and 2.

  • Why the downvote? If the downvoter has an issue with my answer, I would be happy to address it. –  Jul 16 '14 at 13:28
1

I actually think being trained mathematically makes us instinctively use cardinality to decide if a set is bigger than another one. But in a more unsophisticated sense it is perfectly reasonable to say that if an infinite set $A$ is a proper subset of the infinite set $B$ then $B$ is larger than $A$. For example, suppose you are using induction to show some identity holds for every natural number $n$. If you only show it for even $n$, then you are perfectly reasonable to believe that you have only done half the job. The fact that the even natural numbers have the same cardinality as all natural numbers would not necessarily make you think otherwise... even though a few minutes later you'd angrily complain that the movie has got it wrong.

So maybe we are all being wrong by automatically using cardinality as the indicator of the size of a set as the default in everyday life (such as teen romance films.)

Zarrax
  • 44,950
1

I think illustrations work wonders when you are trying to explain and talk about abstract concepts like cardinality.

So for example I would suggest the following one to show that there are as many real numbers as there are between two.

enter image description here

0

For any number between 0 and 2, you can divide it by 2, and get a number between 0 and 1. If you divide two different numbers by 2, you will always get two different answers. Thus, there exists a one-to-one correspondence between the set of numbers between 0 and 1, and the set of numbers between 0 and 2. This means they have the same cardinality.

This argument is basically a less verbose version of the "balls in basket" one, and a less geometrical version of the one with the parallel lines, but I've had success explaining it to English majors in the past.

Tor
  • 183