We rewrite the riddle using prime decomposition.
Notation: $2^{x_1}3^{x_2}5^{x_3}7^{x_4}\leftrightarrow (x_1,x_2,x_3,x_4)$
We have:
$$
(a_1,a_2,a_3,a_4) \odot (b_1,b_2,b_3,b_4) = (c_1,c_2,c_3,c_4)\\
(0,1,0,0) \odot (2,0,0,0) = (3,0,0,0)\\
(2,0,0,0) \odot (0,0,1,0) = (1,0,2,0)\\
(0,0,1,0) \odot (1,1,0,0) = (1,1,1,0)\\
(1,1,0,0) \odot (0,0,0,1) = (0,0,0,2)\\
(0,0,0,1) \odot (3,0,0,0) = ?
$$
We note that the following definition of $(c_1,c_2,c_3,c_4)$ satisfy the given relations:
$$
c_1=a_2+a_3+b_1+b_3-b_2-b_4+2a_4\\
c_2=a_3\\
c_3=a_1+b_2-b_4\\
c_4=a_4+2b_4\\
$$
We then calculate:
$$
(0,0,0,1) \odot (3,0,0,0)=(5,0,0,1) \leftrightarrow 2^57=224
$$
We note though that $a_4$ can appear anywhere and satisfy the given relations namely the riddle can have multiple answers. Knowing the answer is $224$ we can include $a_4$ in the defining relation of $c_1,c_4$.
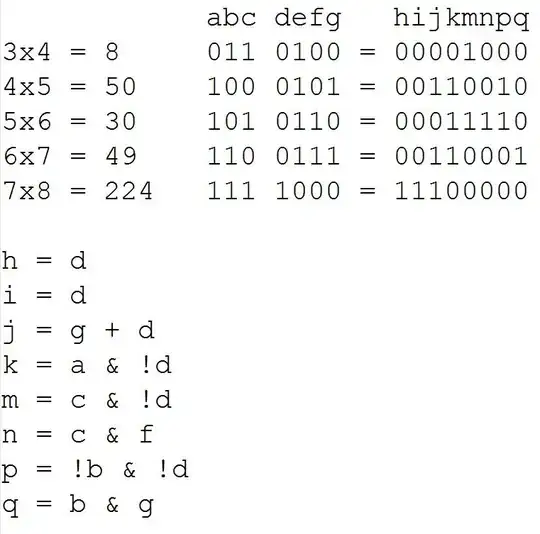
7 x 8 = ?. By definition. – HostileFork says dont trust SE Jul 15 '14 at 07:22x, why not also redefine=and/or the digits? – keshlam Jul 15 '14 at 18:41