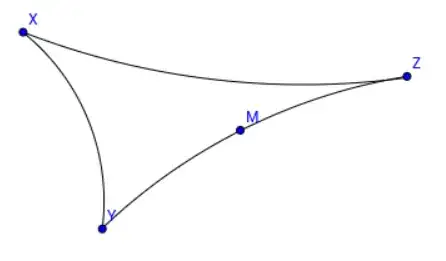
This is not the definition the theory began with; the comparison of geodesic triangles came first. The four-point condition you see has been distilled from that, even shedding the geodesicity assumption. Since a complete CAT(0) space is geodesic, I recommend drawing geodesics between the points you have. The picture will look like this:
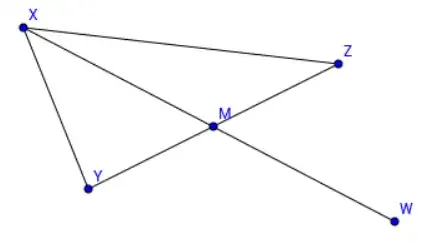
I added an (imagined) point $W$ on the continuation of geodesic $XM$ to emphasize that the condition is a form of the Parallelogram Law. Indeed, multiplying both sides by $4$ an moving $d(y,z)^2$ to the left, you will see the parallelogram law with inequality sign.
What is the meaning of inequality replacing equality? It allows the curvature to be negative, not necessarily zero. (With equality we'd have a flat CAT(0) space.) Negative curvature means geodesic triangles are thin, and therefore the midpoint $m$ can be closer to $x$ than it would be in a flat space: