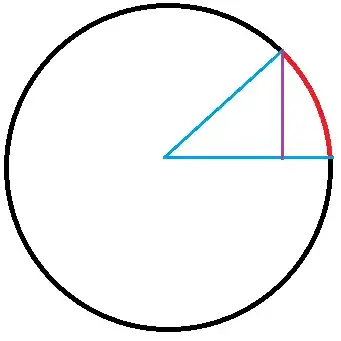1

I have seen in Thomas' Calculus that says to prove $\lim_{x\rightarrow0}\sin x=0$, use the Sandwich Theorem and the inequality $-|x|\le\sin x\le|x|$ for all $x$.

My question is how could the inequality be true? If we derive from $-1\le\sin x\le1$, we could only get $-|x|\le|x|\sin x\le|x|$?

In the textbook it is written that it follows from the definition of $\sin x$ that $-|x|\le\sin x\le|x|$ for all $x$. Is there any easy way to show this?

Thanks for any help.

user71346
  • 4,171
  • 1
    Are you familiar with derivatives? – Peter Franek Jul 12 '14 at 07:47
  • Bartle and Sherbert have a proof using integration. – Clarinetist Jul 12 '14 at 07:50
  • @PeterFranek. Yes. but do we really need derivative here? – user71346 Jul 12 '14 at 07:50
  • @user71346 You do not: you can do it with only geometry. See my answer below. – Adam Hughes Jul 12 '14 at 07:51
  • Any solution would depend on the definition of $\sin$ function. I recommend you go through this and this. – hrkrshnn Jul 12 '14 at 08:06
  • 1
    A user, in a deleted answer, essentially claimed that if $f(a)=g(a)$ and $f(b)\le g(b)$ and $f,g$ are monotonic increasing on $[a,b]$, then $f(x)\le g(x)$ on $[a,b]$. They asked for a counterexample, so here it is: Let $f(x)=x$ and $g(x)=\frac{4}{3}(x-\sin x)$. Then $f(0)=g(0)$ and $f(2\pi)<g(2\pi)$, but $f(x)>g(x)$ strictly on a nice-sized interval $(0,2.4{\rm ish})$. – anon Jul 12 '14 at 08:16

3 Answers3

3

The unit circle is parametrized by $\theta\mapsto(\cos\theta,\sin\theta)$:

$\hskip 1.5in$ circle

Consider an angle $0\le\theta\le\frac{\pi}{2}$, as depicted above. The red line's length is $\theta$, and $\sin\theta$ is the purple length. Since they both travel the same vertical distance but the red one also travels horizontal distance, the red line is longer, hence $\sin\theta\le\theta$. (This can be proved formally with calculus if one so desires.) After $\theta>1$, the angle will forevermore be too much for sine to ever take for any angle. Since $\sin(-\theta)=-\sin\theta$, the claim follows for negative angles too.

anon
  • 151,657
  • I think it's a bit wishy-washy to say "also travels horizontal distance" without quantifying it, Pappus' theorem talks about how two differently shaped objects might have the same geometric volume (in some dimension) despite some being distorted. That's not the case here, but it's less obvious that this is necessarily true, I think. – Adam Hughes Jul 12 '14 at 08:26
  • 1
    @Hugh we're talking about length, not volume. The intuition should be pretty obvious and airtight I think, and I already said one can use calculus if one desired a formal justification. (Indeed, "the shortest distance between two points is a straight line" is proved with calculus. Technically, length of curves is defined with calculus.) The calculus reasoning behind "also moves horizontally" is that if we view the arc as the graph of a function of the triangle side "sideways," then horizontal movement means $f'(y)\ne0$ for some measure of $y$s, hence $\int\sqrt{1+f'(y)^2}dy>\int 1dy$. – anon Jul 12 '14 at 08:44
  • 1
    But I do concede that "the shortest distance between two points" (in Euclidean geometry, of course) is even more intuitively obvious than my "also moves horizontally" idea. – anon Jul 12 '14 at 08:46
  • I completely agree you're right, I meant only that if the student is doing this in a basic course, it might be handy to see why that happens. I agree the intuition is obvious, I make mention of Pappus' theorem because it shows how intuition about geometric quantities can be less airtight. In theory you could appeal to the "shortest distance to a convex set is via orthogonal projection," but that's from a harder subject I suppose. :-) – Adam Hughes Jul 12 '14 at 08:47
2

First of all: you cannot take derivatives (and even if so, your middle one is incorrect) to preserve inequalities. That said, let's go over it:

1) It is enough to show that $\sin x\le x$ when $x\ge 0$ because $\sin x$ is an odd function, so for $x<0$ write $-y=x$ whence the first inequality implies

$$-\sin -y \le y\iff \sin(-y)\ge -y\iff \sin x\ge x$$

Now, to show it for $x\ge 0$ is actually a matter of geometry

Edit: I'm told not everyone can see the photo I'm using. It's available here if that's true for you.

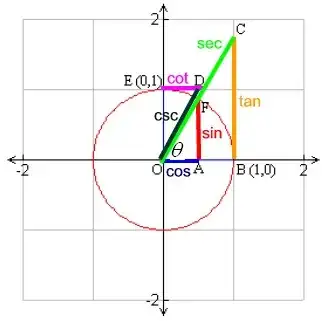
unit circle

Notice that $\sin x$ is the height of the smaller triangle, then draw in segment $FB$. Since $\sin x$ is the length of a leg of a right triangle, it's hypotenuse, $|FB|$ has lenght greater than or equal to $\sin x$. But then the shortest distance between two points is a straight line, so $FB$ is shorter than $\text{arc} FB$, but by the definition of a radian, $|\text{arc} FB|= x$ (the angle is labeled as $\theta$, but we're using $x$. Hence

$$\sin x\le |FB|\le |\text{arc} FB|=x$$

is shown for $0\le x\le {\pi\over 2}$, and for the other positive $x$ it follows from $\sin x\le 1$ independent of $x$.

Adam Hughes
  • 36,777
  • @user71346 The definition of a radian is: length of the arc divided by the radius. So if the angle is $x$ in radians, it means the measure of that arc is x/1 (since the unit circle has radius 1). – Adam Hughes Jul 12 '14 at 08:13
  • Ok. I get it. You use the unit circle, I missed that. Another doubt, what do you mean by smaller triangle and how many triangles you have? which segment is FB? is FB the radius so |FB|=1? Thanks. – user71346 Jul 12 '14 at 08:20
  • @user71346 In the photo there are two triangles: one with the red, dark green, and blue sides is smaller, the one with light green, orange, and gray is the larger one, which you can ignore. F and B are points on the circle (they are labeled) $FB$ is the diagonal line connecting them, not the radius. – Adam Hughes Jul 12 '14 at 08:23
  • I cannot see the picture, maybe thats the problem. But thanks, I have tried to draw it myself. – user71346 Jul 12 '14 at 08:54
  • @user71346 Oh my, that is a problem. http://i.stack.imgur.com/Hm04i.jpg is the photo I'm using. I also put it into the answer. – Adam Hughes Jul 12 '14 at 08:55
  • Thanks. Sorry to say this, but the link does not work. Maybe something is wrong with my computer... – user71346 Jul 12 '14 at 09:01
2

Although an answer without derivatives and integrals is definitely more elegant, you can just use the fact that for $x>0$, $$\sin(x)=\int_0^x \cos y\,dy\leq \int_0^x 1\,dy= x$$ and similarly for $x<0$.

Peter Franek
  • 11,522