1

let us consider following integral

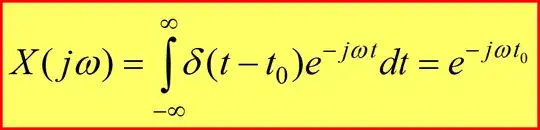
enter image description here

according to property of delta function,we can write this intgeral as

$\int^{t=\infty}_{t=t_0} e^{-j*\omega*t}$

or we can write as

$e^{-j*\omega*t}/(-\omega*t)$ from $t=t_0$ to $t=\infty$,if we calculate it we get

$\frac{e^{-j*w*t_0}} {w*j}$

but i did not understand why is not given in formula denominator part?thanks in advance

dato datuashvili
  • 9,194
  • 1
    I think there has been an abuse of the delta integral here..I think the answer should involve explaining why $\int_{-\infty}^{\infty}\delta(t-t_0)f(t)dt = f(t_0)$. Which would be nice to see :). So in around about why you have asked an interesting question! +1! But this is just my opinion. – Chinny84 Jul 08 '14 at 11:23
  • thanks very much,yes in that case $f(t)=e^{-j\omegat}$ but,during that calculation this part confused me – dato datuashvili Jul 08 '14 at 11:38
  • Please don't use the asterisk for multiplication outside of programming languages. In mathematics, it stands for convolution, not multiplication. – Harald Hanche-Olsen Jul 08 '14 at 11:51
  • i should use \cdot right – dato datuashvili Jul 08 '14 at 11:56
  • Yes, use \cdot, or just don't use a multiplication symbol at all. It is rarely needed. – Harald Hanche-Olsen Jul 08 '14 at 11:56
  • @datodatuashvili I started to write an answer about your derivation but I could not provide a satisfactory (to my standards) explanation of the above identity. So I leave it to others to provide a better answer. But basically the delta function only picks out certain values of the function $f(t)$. – Chinny84 Jul 08 '14 at 11:57
  • $\cdot$ ok thanks in advance – dato datuashvili Jul 08 '14 at 11:57
  • simple you can write dato,it is name,datuashvili it is surname :) – dato datuashvili Jul 08 '14 at 11:59
  • I will bare that in mind Dato. Though auto complete fills that in for me ;). – Chinny84 Jul 08 '14 at 12:01

1 Answers1

2

You might want to take a look at the answers to this question.

In less technical language: The delta “function” has the defining property that $$\int_{-\infty}^\infty \delta(x)f(x)\,dt=f(0)$$ for any continuous function $f$. Substituting in $x=t-t_0$ with $f(x)=e^{-j\omega x}$ immediately yields the desired result.

Your rewrite of the integral “according to property of delta function” is not according to any property of the delta known to me.

Community
  • 1
Harald Hanche-Olsen
  • 31,960
  • That was the answer I was going to put but is it out of the scope of this particular question to why this integral holds? I do not want to overload/monkey patch on another question if it is not necessary :). – Chinny84 Jul 08 '14 at 12:15
  • @Chinny84 I was puzzled about your reluctance to post an answer. Not sure what you mean by “out of scope”. I would have liked to link to an answer that is more directed at the OP's level, but a quick search did not reveal such an answer. (Perhaps I gave up too easily.) … Oh, just saw your followup comment. As you say, never mind … – Harald Hanche-Olsen Jul 08 '14 at 12:26
  • I think it was a miscommunication. I wasn't to sure if the answer needed to explain why the integral with the delta function holds. But having a look at the link you provided it seems it would be too technical. Don't worry, I think I am just over analysing the question :). Great answer :). – Chinny84 Jul 08 '14 at 12:42