0

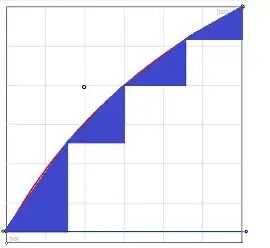
I need to find the length of this curve:

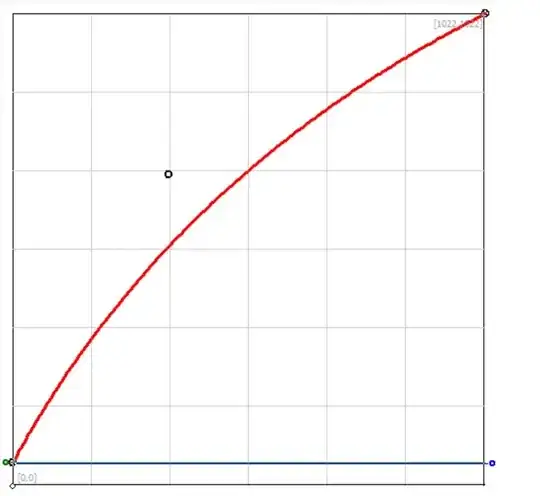
enter image description here

I don't have a function but I do have 3 sets of coordinates:

$(0, 51)$, $(337, 674)$, and $(1022, 1022)$

The $(337, 674)$ set refers to the tangent and it makes the curve be equidistant.

I know nothing beyond basic math, however I'm working on this tablet pressure sensitivity thing and there's no other way out. I have to find the length of the curve or figure out the function which creates that curve.

Thank you fellas!

Peter Woolfitt
  • 21,114
user326547
  • 1
  • 1
    Plot it with the same $x,y$ axis scale and measure it with a string. – copper.hat Jul 07 '14 at 17:34
  • There are many many curves which could fit this. Do you have any more restrictions on the type of curve you want? For example, it could be part of a parabola, or part of a circle. – Peter Woolfitt Jul 07 '14 at 17:36
  • Could you explain more about what the $(337,674)$ point means? – Empy2 Jul 07 '14 at 17:45
  • I don't understand what do you mean. The curve is there already. The function I'm looking for should plot the exact same curve as the one in the image I posted. I wouldn't know if it's part of a circle or parabola. – user326547 Jul 07 '14 at 17:45
  • @Michael That point shows the exact half of the curve. I don't know the appropriate name for it, but think of it as the "tension" point of the curve, as it was being pulled to the upper left corner. – user326547 Jul 07 '14 at 17:50
  • 1
    @user326547 Since the thickness of the curve is nonzero, and the image is pixelated, there are infinitely many curves that would look like "the exact same curve as the one in the image" and they can have different arc lengths. – 2'5 9'2 Jul 07 '14 at 17:54
  • Is this a Bezier curve using that point off the curve for the interpolation? – 2'5 9'2 Jul 07 '14 at 18:05
  • @user326547 Is this what the curve should be? It's what I first thought of when I read "as if it was being pulled to the upper left corner" ... – Zubin Mukerjee Jul 07 '14 at 18:08
  • Some more information about the context could be helpful. Is this some sort of programming task? Or homework? It basically looks like a simple bezier curve, so http://math.stackexchange.com/questions/12186/arc-length-of-b%C3%A9zier-curves might be helpful, but it seems like there's hardly a "handy" closed form, and you probably should use an approximation (picking some points on the curve and adding their distances) – Marco13 Jul 08 '14 at 08:13

4 Answers4

2

If you know (or can make good estimates for) other points on the curve, you can make decent approximations using triangles.

E.g. if you divide it up into 1, 2, or 4 triangles (you can use however many you want; more triangles is more accurate), it might look like this:

One triangle!Two triangles!Four triangles

To find the length of the curve, just add the lengths of the hypotenuses of the triangles. For each triangle, just take the $x$ length and $y$ length and plug them into $L = \sqrt{x^2 + y^2}$.

Scott Caldwell
  • 554
  • +1, but the triangles are a little superfluous. You could just say "pick a number of points on the curve, and add up the distances between them". –  Jul 07 '14 at 18:26
0

I'm not sure exactly what you mean when you claim not to know anything beyond "basic math," but staying on the safe side, I think your best bet is to follow copper.hat's suggestion and just use a string. It looks like your window is already square, so just measure across the square, which will give you a conversion factor between string length (in cm or whatever other physical units you like) and the abstract measure of distance employed in the diagram (you already know that the square measures 1022 across). Then, overlay a string onto the curve, cut it or mark it up, and determine its length in physical units. Then, convert that with the factor you determined earlier.

hexaflexagonal
  • 1,426
  • I see, but wouldn't there be any other way at all? A more precise way? I can't believe Math hasn't come up with a way to solve my issue. – user326547 Jul 07 '14 at 17:47
  • 1
    To be honest, I don't know what you mean when you say "refers to the tangent and it makes the curve be equidistant." It's unclear wording. Can you be more precise? Then I might be able to go for a more precise answer. – hexaflexagonal Jul 07 '14 at 17:49
  • Its mathematics, not magic :-). – copper.hat Jul 07 '14 at 17:49
  • @DivergentQueries I'm aware the wording is unclear. I'll do my best to explain. This set of coordinates, 337,674, is the very "crest" of the curve. And that same point divides the length of the curve in half. – user326547 Jul 07 '14 at 18:02
  • @user326547 I think a more precise way to say what you're saying is that the point $(337, 674)$ is the point on the curve that is furthest from the line connecting the other two points, and also the point that bisects the length of the curve. Even so, there are multiple curves that satisfy both of these requirements, and so the information you've given isn't sufficient for an exact answer. – Zubin Mukerjee Jul 07 '14 at 18:15
  • @ZubinMukerjee Exactly! So you think there's really no way to extract a function or the curve's length just by looking at that graph an making use of the info I gave? What kind of info should I try to bring so it's enough to solve? – user326547 Jul 07 '14 at 18:27
  • Honestly, if you're looking for an exact answer, then you're probably going to need to know what the function is. If, however, you're happy with an approximate length, then many of the answers already given can do that. – Zubin Mukerjee Jul 07 '14 at 18:34
  • It actually doesn't look like the point $(337, 674)$ is on the curve at all. Isn't it the third dot on your diagram (the one not in a corner)? – hexaflexagonal Jul 07 '14 at 18:36
0

Fits a quadratic function $f(x) = ax^2 + bx + c$ as follow: $$ \begin{cases} y_1 = f(x_1) = ax_{1}^2 + bx_1 + c\\ y_2 = f(x_2) = ax_{2}^2 + bx_2 + c\\ y_3 = f(x_3) = ax_{3}^2 + bx_3 + c\\ \end{cases} $$ Solve the linear system to find $a$, $b$ e $c$. Then use the formula $$ L = \int_{x_1}^{x_3}\sqrt{1 + f^{\prime}(x)^2} \ dx $$ Note that, $f^{\prime}(x)^2 = (2ax + b)^2$. Thus, $$ L = \int_{x_1}^{x_3}\sqrt{(2ax + b)^2 + 1} \ dx $$ Write $2ax + b = \tan \theta$ and make the substitution of variables.

Mathsource
  • 5,393
-2

Use a Riemann sum for the arc length integral, making estimates of the slope at test points.

Sorry if you are unfamiliar with that vocabulary, but you say "I can't believe Math hasn't come up with a way to solve my issue", and in fact it has, and it uses this vocabulary.

2'5 9'2
  • 54,717
  • Unfortunately, vocabulary cannot change the fact that there is insufficient information. The curve could be part of a parabola. It could be part of a catenary. It could be very many things, without more information than three points and a graph (that can really only give us a rough visual). Your answer is not very helpful as it is now (-1). – Zubin Mukerjee Jul 07 '14 at 18:10
  • @ZubinMukerjee These down votes are ridiculous. The answer says "making estimates" of the slope. No formula is necessary for that. – 2'5 9'2 Jul 07 '14 at 18:29
  • There is plenty of information for making an estimate of the arc length, which is all this answer purports to do, which is all any of the answers here do. – 2'5 9'2 Jul 07 '14 at 18:31
  • What function do you propose to use for your Riemann Sum? There is none given ... It is in fact the case that "math hasn't come up with a way" to solve OP's problem, because OP didn't give enough information. – Zubin Mukerjee Jul 07 '14 at 18:33
  • @ZubinMukerjee You don't have to have a formula for $f$. You just need to estimate $f'$ at the test points. Here is a crude $n=2$ Riemann sum using left endpoints: $\int_a^b \sqrt{1+f'(x)^2},dx\approx \sqrt{1+(2)^2}\cdot511+\sqrt{1+(1)^2}\cdot511$. All you need to do is use the image to estimate slopes at the test points. It sounds like your understanding of Riemann sums is too closely linked to the formulaic representation of a function. – 2'5 9'2 Jul 07 '14 at 18:37
  • Hmm. I suppose your second paragraph made it sound as though the use of Riemann sums would both be necessary for OP to solve the problem, and would give an exact answer somehow. Neither is the case. The context in which OP made his comment about math "not having a solution" was clearly about an exact answer. In any case, I'd be happy to remove my downvote if I could. – Zubin Mukerjee Jul 07 '14 at 18:47