I defined a function $f$ as follows:
Let $I_{n,k}=\left(x_1,x_2\right)$ the removed open interval in step $n$ at position $k$ of the $\frac{1}{3}$-cantor set and $J_{n,k}=\left(y_1,y_2\right)$ the removed open interval in step $n$ at position $k$ of a arbitrarily fat cantor set. Map the closure of $I_{n,k}$ onto the closure of $J_{n,k}$ like:
$$f:clo(I_{n,k}) \rightarrow clo(J_{n,k}): x\mapsto \begin{cases}f(x):=y_1&x=x_1\\f(x):=y_2&x=x_2\\f(x):=\frac{y_2-y_1}{x_2-x_1}\cdot x & x\in\left(x_1,x_2\right)\end{cases}$$
Due to the construction $f$ is bijective and continuous at $\left(x_1,x_2\right)$ for every $I_{n,k}$ but I struggle with the continouity at the endpoint of the intervals $I_{n,k}$. The fact that I want to map onto the fat cantor set it's not possible to argue with $\left(\frac{1}{2}\right)^n$. What am I missing?
For example:
$clo\left(I_{1,1}\right)=clo\left(\left(\frac{1}{3},\frac{2}{3}\right)\right)=\left[\frac{1}{3},\frac{2}{3}\right]$ maps to $clo\left(J_{1,1}\right)=\left[y_1,y_2\right]$ with the definition of $f$, repeating for every $n \in \mathbb{N}$ with the inherent intervals.
That's what I am thinking:
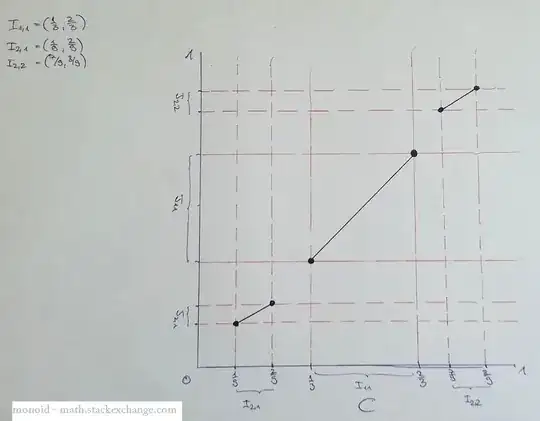
So $f\left( \frac{1}{3}\right)=y_1$, $f\left(\frac{2}{3}\right)=y_2$ and for all $x \in I_{1,1}$ is $f\left(x\right)=\frac{y_2-y_1}{\frac{2}{3}-\frac{1}{3}}=3(y_2-y_1) \cdot x$.