injective curve inside curve

Question

I am struggling to prove the following intuitive result:

Take $\phi:[a,b]\rightarrow \mathbb{R}^{n}$ a continuous mapping with $\phi(a)\neq\phi(b)$. Then there is a continuous injective mapping $\phi_{0}$ with image contained in $\phi([a,b])$ such as $\phi_{0}(a)=\phi(a)$ and $\phi_{0}(b)=\phi(b)$.

I found this statement in Falconer, The geometry of fractal sets, with a sadly incorrect proof, which went as follows.

"Take the collection $\mathcal{C}$ of proper intervals $I_{x}$ of the form $[t_{1},t_{2}]$ with $\phi(t_{1})=\phi(t_{2})=x$ who are contained in no other intervals of the same form. Since it is a collection of countably many proper disjoint closed intervals, we can find a continuous surjective increasing function $f:[a,b]\rightarrow [a,b]$ such as $f(t_{1})=f(t_{2})$ if and only if $t_{1}=t_{2}$ or if $t_{1},t_{2}$ are in a same interval of $\mathcal{C}$. Then it is easy to check that $\phi_{0}$, defined by $\phi_{0}(u)=x$ if $f^{-1}(u)=I_{x}$ and $\phi_{0}(u)=\phi(f^{-1}(u))$ otherwise, satisfies our requirements."

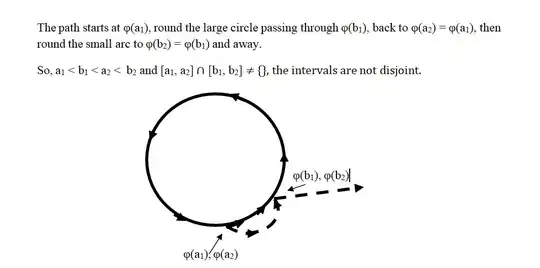
The problem with that proof is that though the intervals of $\mathcal{C}$ are indeed proper and closed, they are not necesarily disjoint. I can't reproduce the drawing here but it is not too difficult to show a curve in $\mathbb{R}^{2}$ with two double points $x,y$ such as $\phi(a_{1})=\phi(a_{2})=x$, $\phi(b_{1})=\phi(b_{2})=y$, and $a_{1} < b_{1} < a_{2} < b_{2}$.

I don't know how to complete the proof (I even tried with Zorn's lemma), if you have any ideas they are welcome.

---

Here's a diagram ...
Since the intervals are not necessarily disjoint they aren't necessarily countable either.

Answer 1

How about this, a way to make Zorn's Lemma work.

Let $\mathcal{K}$ be the collection of all nonempty closed subsets $K \subset [a,b]$ with the following properties:

• The first point $a_K$ of $K$ satisfies $\phi(a)=\phi(a_K)$.
• The last point $b_K$ of $K$ satisfies $\phi(b)=\phi(b_K)$.
• For each interior component $(c,d)$ of $[a,b]-K$ we have $\phi(c)=\phi(d)$.

This set $\mathcal{K}$ is nonempty because $[a,b] \in \mathcal{K}$.

Lemma: Consider a subset $\{K_i\}_{i \in I} \subset \mathcal{K}$ which is linearly ordered by inclusion: the index set $I$ is ordered and if $i<j$ then $K_i$ is a proper subset of $K_j$. Then the intersection $K_\infty = \cap_i K_i$ is an element of $\mathcal{K}$.

Proof: Start with the fact that $K$ is nonempty, being a nested intersection of compact nonempty sets. Consider an interior component $(c,d)$ of $[a,b] - K_\infty$, for all sufficiently small $i \in I$ there exists a component $(c_i,d_i)$ of $[a,b] - K_i$ such that as $i \in I$ decreases we have $\lim c_i=c$ and $\lim d_i = d$. Since $\phi(c_i)=\phi(d_i)$ , by continuity it follows that $\phi(c)=\phi(d)$, and so $K_\infty \in \mathcal{K}$. A similar argument shows that $\lim a_{K_i} = a_{K_\infty}$ and $\lim b_{K_i}=b_{K_\infty}$ and so by continuity $\phi(a_{K_\infty}) = \phi(a)$ and $\phi(b_{K_\infty}) = \phi(b)$.

Applying Zorn's Lemma, the set $\mathcal{K}$ has a minimum element $K$. This $K$ has the following property: for all $c<d \in K$, if $\phi(c)=\phi(d)$ then $(c,d)$ is an interior component of $[a,b]-K$. For if this were not so, then one could find a smaller element of $\mathcal{K}$ by removing all points of $K \cap (c,d)$.

Also $K$ has no isolated point. For suppose $p \in K$ is isolated. If $p \ne a_K,b_K$, then there would exist components $(c,p)$ and $(p,d)$ of $[a,b]-K$ and so $\phi(c)=\phi(p)=\phi(d)$, implying that $K-\{p\} \in \mathcal{K}$. And if $p=a_K$ then there is a component $(p,d)$ of $[a,b]-K$ and so $\phi(d)=\phi(p)=\phi(a)$ implying again that $K-\{p\} \in \mathcal{K}$. Similarly if $p=b_K$.

Now define a quotient space $J$ of $K$: for each component $(c,d)$ of $[a,b]-K$ we identify $c$ to $d$, and no other identifications are made. This quotient space $J$ is homeomorpic to the interval with endpoints equal to the images of $a,b$ under the quotient map $K \to J$. The restriction of $\phi : [a,b] \to \mathbb{R}^n$ to $K$ induces the desired injective path $J \mapsto \mathbb{R}^n$.

Addendum: The statement about the quotient of $K$ being an interval is a consequence of the Bing shrinking criterion, applied to the interval $[a_K,b_K]$ with the partition whose elements are as follows: the closed interval $[c,d]$ for each interior component $(c,d)$ of $[a,b]-K$; and every remaining point of $[a_K,b_K]$ forms a singleton partition element.