5

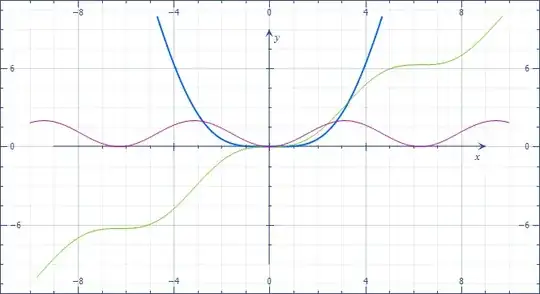
I am having a problem in showing that $\cos x -1+\dfrac{x^2}{2!} \geq 0$ for every $x\in \mathbb{R}$.

I have tried the following:

I understand that $\dfrac{x^2}{2!}$ is always non negative. But $\cos x-1$ can be negative. So I can't conclude anything about their sum.

I know that $\cos x=1-\dfrac{x^2}{2!}+\dfrac{x^4}{4!}-\ldots$ so that $\cos x-1+\dfrac{x^2}{2!}=\dfrac{x^4}{4!}-\dfrac{x^6}{6!}+\ldots$ but how do I show that the series in RHS is non-negative? I need some help.

Martin Sleziak
  • 53,687
Dimpu
  • 55

5 Answers5

6

Notice that $f(x)=\cos(x)-1+\frac{x^{2}}{2}$ is even so it suffices to show that it is non-negative on the non-negative reals. Differentiating we get $f'(x)=x-\sin(x)\ge0$ so $f$ is increasing on the non-negative reals. Hence, $f(x)\ge f(0)=0$.

user71352
  • 13,038
  • oh thanks ! Thats a good way! So I have to take the help of calculus here :) – Dimpu Jul 03 '14 at 07:01
  • You're welcome! I'm not sure if you have to make use of calculus but I like to when I can. – user71352 Jul 03 '14 at 07:05
  • 1
    You also have to prove that $x-\sin x>0$ ! –  Jul 03 '14 at 07:05
  • Perhaps I misunderstand. Why do we need that the function is strictly increasing? The inequality we desire is non-strict. – user71352 Jul 03 '14 at 07:10
  • @user71352 .. Also, $f$ is decreasing on the negative reals. So, $x<0\Rightarrow f(x)>f(0)$. Thus $\cos x-1+x^2/2!\geq 0$ for every real $x$ – Dimpu Jul 03 '14 at 07:21
  • You could argue that way. In my answer I simply noted that the function $f(x)=\cos(x)-1+\frac{x^{2}}{2}$ is even so if I knew the inequality for non-negative reals then I obtain it for the non-positive reals since for $x\ge0$ $f(-x)=f(x)\ge0$. – user71352 Jul 03 '14 at 07:28
  • This question should have the calculus tag instead of the precalculus one. I dislike when I am looking for preCalculus answer (assuming that the OP does not know Calculus) and the OP accepts a Calculus answer. Good answer though. – Taladris Jul 03 '14 at 07:37
  • @Taladris .. Ya I have edited the tag. Actually I am quite new to calculus and I didn't think that I will need it here :) – Dimpu Jul 03 '14 at 07:40
  • @user71352: "Perhaps I misunderstand": What Yves really meant was, you also have to prove that $x - \sin x \ge 0$ for $x \ge 0$. Which is almost as hard as the original question! So this answer is deficient, in my opinion. – TonyK Jul 03 '14 at 14:16
4

By the Maclaurin formula and for $x\in\Bbb R$ there's $\theta\in(0,1)$ such that

$$\cos x=1-\frac{x^2}{2}\cos(\theta x)\ge 1-\frac{x^2}2$$ and the result follows.

3

From $\cos^2x+\sin^2x=1^*$, we have $|\cos x|\le1$, and $$\color{magenta}{f''(x)}=1-\cos(x)\ge0.$$ The zeroes of $f''$ are isolated, at $x=2k\pi$.

This implies that $\color{green}{f'(x)}=x-\sin(x)$ is strictly monotone increasing, for all $x$, except at $x=2k\pi$. As $f'(0)=0$, this is the only real root of $f'$.

This implies that $\color{blue}{f(x)}$ is strictly decreasing for $x<0$ and strictly increasing for $x>0$. The global minimum of $f$ is $f(0)=0$, and $$\cos x-1+\frac{x^2}2\ge0.$$

enter image description here

*$\cos^2x+\sin^2x=(\frac{e^{ix}+e^{-ix}}2)^2+(\frac{e^{ix}-e^{-ix}}{2i})^2=\frac{e^{2ix}+2+e^{-2ix}}4-\frac{e^{2ix}-2+e^{-2ix}}4=1$

2

Perhaps this can be considered a "precalculus" answer.

There are geometric proofs that $|\sin x| \le |x|$.

(for instance, see this: https://math.stackexchange.com/a/75151/1102)

Combine that with $\cos 2x = 1 - 2\sin^2 x$, we get your inequality easily:

$$ \sin^2 (x/2) \le x^2/4 \implies 1 - 2\sin^2 (x/2) \ge 1 - x^2/2 \implies \cos x \ge 1 - x^2/2$$

Community
  • 1
Aryabhata
  • 82,206
0

Once you've proven the result for $x \in \mathbb{R}^{+}$ with the above-mentionned geometric evidence, just use the fact that your function is even to get your proof done in $\mathbb{R}^{+} \cup \mathbb{R}^{-}$, which is $\mathbb{R}$.

BusyAnt
  • 21