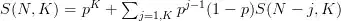2

Each event has two possible outcomes: a and b.

Each event is independent.

Outcome a has $X\%$ chance of happening.

If we run $Y$ number of such events, what are the chances of getting $K$ outcomes a in a row, at least once?

To put it in practical terms imagine a series of coin tosses. Each coin toss has two possible outcomes: a = heads and b = tails. Outcome a = heads has a chance of $50\%$. If we run $Y = 100$ number of coin tosses, what are the chances of getting $K = 10$ outcomes a=heads in a row, at least once?

I'm using the practical example only so I can express the idea more clearly. I'm interested in finding out the general formulas and computations so that I can run the calculations for any $X$, $Y$, or $K$.

I would also be very interested in knowing how the probabilities would change if the events would not be independent. What if the more outcomes a we have in a row the bigger the chance of getting an outcome a in the next event? What if it's the other way around, and the more outcomes a in a row we have the lower the chance of getting another a?

Cristian
  • 173
  • See also http://math.stackexchange.com/questions/59738/probability-for-the-length-of-the-longest-run-in-n-bernoulli-trials/59749#59749 –  Nov 26 '11 at 17:24

1 Answers1

1

I eventually found the answer to my question on AskAMathematician

The formula I was looking for is:

enter image description here

where S(N,K) is the probability of a run of K events in a row at least once in a series of N trials. So N is the total number of trials, K is the number of events in a row, and p is the probability of each such independent event. More explanations can be found on the aforementioned website. Another useful resource is the Wolfram website which features a nice section on runs and probabilities.

The formula is very hard to calculate by hand when big numbers are involved and a special calculator is the only solution. If you are interested in some programming code which could do the calculations for you, you can go to the askamathematician website and see their python code, or you can use the C# function written by me below:

public double s(int n, int k, double p)
{
    double result;
    double[] x = new double[10000];

    x[0] = Math.Pow(p, k);
    int i = 1;

    while (n > k)
    {

        double sum = 0; int l;
        if (i - k < 0) l = 0; else l = i - k;
        for (int j = i; j > l;j--)
        {
            sum += (1-p) * Math.Pow(p, 0 + i - j) * x[j-1];
        }
        x[i] = Math.Pow(p, k) + sum;

        i++;
        n--;
    }

    result = x[i-1];


    return (result);
}
Cristian
  • 173