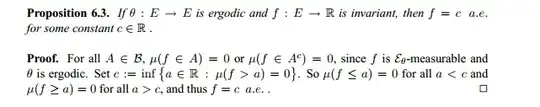
I understand the first two sentences of the proof, however I cannot see how the third and final sentence holds. Why should $\mu(f \leq a)=0$? Surely it should be non-zero as c is defined as the infimum that $\mu(.)=0$? I equally don't understand how $\mu(f \geq a)$ should equal $0$ if $\mu(f \leq a)=0$.