2

How to solve this:

$$\displaystyle\int \bigg(\small\sqrt{\normalsize x +\small\sqrt{\normalsize x +\small\sqrt{\normalsize x +\sqrt{x}}}}\;\normalsize\bigg) \;dx$$

Zev Chonoles
  • 129,973
Anonymous
  • 39
  • 2
    Seems like this is a tough one, at least mathematica cannot find it http://www.wolframalpha.com/input/?i=Integrate[Sqrt[x+%2B+Sqrt[x+%2B+Sqrt[x%2BSqrt[x]]]]%2Cx] – Listing Nov 24 '11 at 08:07
  • 3
    I don't think that integral is huge enough. – mathmath8128 Nov 24 '11 at 08:07
  • 2
    What does it mean to "solve" an anti-derivative? – Ryan Budney Nov 24 '11 at 08:25
  • You could try a series expansion. – Raskolnikov Nov 24 '11 at 08:37
  • 2
    I can help with $I=\int \sqrt{x+\sqrt{x}}dx$: Let $u(x)=\sqrt{x}$. Then $dx=2\sqrt{x}du$ and $I$ becomes $I=\int \sqrt{u^2 + u}2udu$. We integrate by parts and $I=2[\frac{u}{2\sqrt{u^2+u}}-\int \sqrt{u^2+u}du]$. Let $J=\int \sqrt{u^2+u}du$. Then $J=\frac{1+2u}{4}\sqrt{u^2+u}-\frac{1}{8}ln |2u+1+2\sqrt{u^2+u}|+c$ (from tables). – Pantelis Sopasakis Nov 24 '11 at 09:53
  • Just let $u=\sqrt{x+\sqrt{x+\sqrt{x+\sqrt{x}}}}$ is OK. Then you will get $x$ in terms of polynomial of $u$. WolframAlpha canot solve it because the process time is excessed. – doraemonpaul Jul 13 '12 at 11:39

1 Answers1

4

While this is not an answer, I posted it as an answer so that I can attach the graph. On the graph you can see how close the 2 functions are. Using this fact may help.

The Black graph is the original function and the Red graph is for the approximate function.

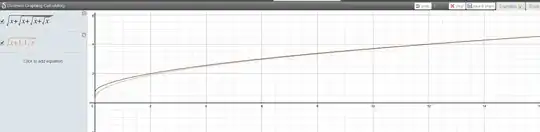
enter image description here

A better approximation for the function $f(x)=\displaystyle\bigg(\small\sqrt{\normalsize x+\small\sqrt{\normalsize x+\sqrt{ x+\sqrt{x}}}}\;\normalsize\bigg)$ is:

$0.5(1+\sqrt[]{1+4x})$

This approximation was obtained from Nested Radicals, This formula is an exact value for the infinite case, so it may be used as an approximation only in your case.

A picture of the 2 functions is shown below. The Black graph is the original function and the Red graph is for the approximate function.

enter image description here

NoChance
  • 6,427
  • How did you come up with this approximation? Can you post the proof that it asymptotically approximates the given function? – Pantelis Sopasakis Nov 24 '11 at 10:28
  • In fact I can't claim that it an optimal approximation since I came across it by plotting various curves and noticed that this one was among the better ones. The main point I wanted to show is that there may be a good approximation for the original function that may help. – NoChance Nov 24 '11 at 10:36