Are there 2D analogues for integer division and modular arithmetic?

Question

Let's say you have a "parallelogram" of points $P = \{(0, 0), (0, 1), (1, 1), (0, 2), (1, 2)\}$. This parallelogram lies between $u = (2, 1)$ and $v = (-1, 2)$.

Then for any point $n \in \mathbb{Z}^2$, you can write

$n = dQ + r$,

where $Q = \begin{pmatrix} u\\ v\end{pmatrix} = \begin{pmatrix}2 &1 \\ -1 &2\end{pmatrix}$, and $r \in P$.

As an example, I try to show how these things relate in the following image:

$$(3, 5) = (2, 1)\begin{pmatrix}2 &1 \\ -1 &2\end{pmatrix} + (0, 1)$$

Here is another image, showing that $Q$ need not be in the form $\begin{pmatrix}a & -b \\b&a \end{pmatrix}$.

$$Q = \begin{pmatrix}-4 & 2 \\ 1 & 2\end{pmatrix}$$

My question is: is type of thing studied (for general parallelograms), and what is it called?

I have many questions about it, and do not know where I can find more information. For example: how do you find $d$ and $r$, does it make sense (and what is the use) of defining $n_1 \equiv n_2 \pmod Q$ if $n_1$ and $n_2$ have the same "remainder" when "divided" by $Q$, and if so, what rules govern this system; what is the situation on a hexagonal lattice; what if $P$ is not a parallelogram.

---

Background

The reason I'm interested in this is that I use it in a large variety of algorithms, including sub-sampling of grids, maze generation, and using grids to represent more complicated things (for example, using a hex grid to represent a triangular grid + vertices).

Although I have ways to calculate $d$ and $r$ given $n$ and $Q$, my algorithms are rather clumsy, and "hacked together". I'd like to back this with some theory, perhaps simplify and optimize the algorithms, and be in a better position to design related algorithms and be able to justify it mathematically.

Answer 1

Rather than using matrices in the quotient there, it may be a better idea to use complex numbers. There, the division algorithm uses complex multiplication instead of matrix multiplication as you have used. For the square lattice, the relevant object is the domain of Gaussian Integers. For the hexagonal (triangular) lattice, you need the Eisenstein integers. Both are Euclidean domains, which means that division with remainder as you have described is possible.

In order to actually compute the division in the Gaussian integers (square lattice), the following is a start:

Let $z,w \in \mathbb{Z}[i], w\not=0$. We want to find $q,r\in \mathbb{Q}$ such that $z = qw + r$ and $|r| < |w|$, or equivalently, $q$ such that $|\frac{z}{w} - q|< 1$.

If $\frac{z}{w} = x + iy$ where $x,y \in \mathbb{Q}$, take $q = [x] + i[y]$ (where $[x]$ denotes the integer closest to $x$), then indeed we have that $|\frac{z}{w} - q|\leq |(x - [x]) + i(y - [y])|\leq \sqrt{\frac{1}{2^2} + \frac{1}{2^2}} = \frac{1}{\sqrt{2}} < 1$. Hence $q = [x] + i[y]$ and $r = z - qw$ work.

For the Eisenstein integers, you should be able to devise something very similar.

If for some reason you need to have this in the language of matrices, just remember that multiplication of a complex number $x+iy$ by the complex number $a + bi$ is equivalent to multiplication of the vector $\begin{pmatrix}x \\ y\end{pmatrix}$ by the matrix $\begin{pmatrix} a & -b \\ b & a\end{pmatrix}$, so the above method can be converted to vectors in $\mathbb{Z}^2$ and matrices if you prefer.

Answer 2

Finding $d$ and $r$: I don't know whether this is more or less clumsy than your existing algorithm: to write $n$ as $dQ+r$ for a given $Q,$ you can compute $x=nQ^{−1}.$ Then compute the floor of the elements of $x$ to get $d,$ and compute $n−dQ$ to get $r.$ To keep the arithmetic integer, if desired, you can write $Q^{−1}=\mathrm{adj}(Q)/\det Q.$ Since the adjugate matrix, $\mathrm{adj}(Q),$ is integer, the vector $y=n\,\mathrm{adj}(Q)$ is integer, and $d$ can be obtained by dividing $y$ by $\det Q$ using integer division. This algorithm applies in dimensions higher than $2$ as well.

To verify that this works, the first key idea is that $x\mapsto xQ$ is a linear map. So $(ax+by)Q=a(vQ)+b(uQ)$ for any vectors $x$ and $y$ and scalars $a$ and $b.$ This means that the unit square spanned by $e_1=(1,0)$ and $e_2=(0,1),$ that is, the set $\{ae_1+be_2\mid 0\le a,b<1\},$ is sent to your parallelogram, that is, to $\{au+bv\mid 0\le a,b<1\},$ under this map.

The second key idea is that $Q$ is invertible. Consider a point $n=dQ+r,$ where $d$ is an integer vector and $r$ is in your parallelogram. Multiplying by $Q^{-1}$ from the right on both sides, we get $nQ^{-1}=d+rQ^{-1}.$ To show that the algorithm works, that is, to show that the floor of this expression equals $d,$ we need to show that all components of $rQ^{-1}$ lie in the interval $[0,1)$. But we have established that $Q$ sends the unit square to your parallelogram. Since $Q^{-1}$ is invertible, it reverses the process, sending points in the parallelogram to the unit square, which is what we needed to show.

The intuition is that $dQ,$ with $d$ an integer vector, is a lattice point. If your parallelogram is translated to this lattice point, the other three vertices of the translated parallelogram are $(d+e_1)Q,$ $(d+e_2)Q,$ and $(d+e_1+e_2)Q.$ Points in the interior of the translated parallelogram are $xQ,$ where, writing $d=(d_1,d_2),$ $x=(x_1,x_2),$ we need $d_1<x_1<d_1+1,$ $d_2<x_2<d_2+1.$ So the floor of $x_1$ and $x_2$ are $d_1$ and $d_2.$

Where do $P$ and $Q$ come from? I'm not sure from your question whether you are starting from the set $P$ and obtaining $Q$ from it, or starting from $Q$ and computing $P$ from it, or whether both $P$ and $Q$ are given data. It seems to me that if you need to compute $P$ from $Q,$ that's a slightly tricky problem—harder, in my opinion than computing $d$ and $r$ from $Q.$ (One can always use the algorithm for finding $r,$ combined with brute force, but for a very long and thin parallelogram this might not be efficient.)

Note that the same lattice can be described by infinitely many different matrices $Q.$ Specifically, a matrix $Q'=QU,$ where $U$ is an integer matrix with determinant $\pm1,$ produces the same lattice as $Q$ does. Matrices like $U$ are called unimodular matrices. The product of two unimodular matrices is a unimodular matrix, so unimodular matrices form a group. This is essentially the modular group (up to questions about whether determinant $-1$ is allowed, and whether $U$ and $-U$ should be considered equivalent).

In your position, however, I suspect a study of the modular group might not be the most direct approach to answering the questions you're interested in. I would focus more on the computational, algorithmic literature. I don't have a good recommendation, unfortunately, but you might start by reading up on the LLL algorithm. Even if you don't have an immediate use for that algorithm, it is likely that someday you will. But more to the point, you'll probably pick up a lot of useful insights about how people who compute with lattices think about things.

To finish the discussion above: if you use $Q'$ instead of $Q,$ you have a different parallelogram, and therefore a different set of points—call it $P'.$ You can create a dictionary between $P$ and $P',$ using the algorithm for finding $r.$ (Note that $P$ and $P'$ will have the same size; correspondingly, $Q$ and $Q'$ will have the same determinant, up to sign.)

Fundamental region not a parallelogram: If you want to do the same thing for a hexagonal tiling, say, you can proceed in a similar way. (There's a bit of a terminology issue here: a hexagonal tiling is not a lattice: mathematically, a lattice is a group, which requires that the sum of two lattice vectors be a lattice vector. This is not true of the vertices of a hexagonal tiling.) Note that in a parallelogram tiling, the four vertices are equivalent. So $P$ contains one vertex and a bunch of interior points. In the hexagonal case, the six vertices are not all equivalent; there are two equivalence classes, consisting of three vertices each. So $P$ will contain two vertices and a bunch of interior points.

You can always define a parallelogram-shaped fundamental region that gives the same thing as the hexagonal one. Then use the algorithm above for finding $r.$ Finally you will need a dictionary mapping the points of the fundamental parallelogram to the points of the fundamental hexagon. Devising an algorithm to produce such a dictionary may be a bit awkward, but once you have the dictionary, things are straightforward.

Answer 3

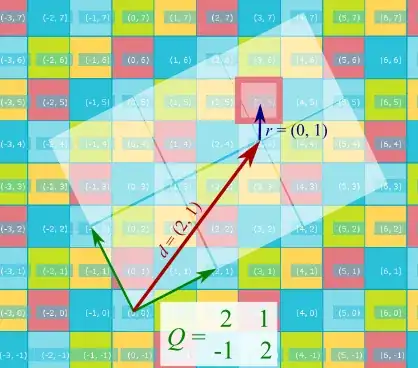
At the risk of stating the obvious, this answer provides a formula for $\vec{d}Q$ and $\vec{r}$. (after writing it i realize its kind of extra-complicated especially compared to Will Orrick's answer of inverting a matrix and, also calculating r directly instead of using n minus Qd but i thought it was an interesting comparison none the less)

Vectors and Wedges

To begin, let us imagine that we consider the situation as vectors. Also note that for two 2d vectors $\vec{a}$ and $\vec{b}$ the Wedge Product is defined as the signed area of parallelogram formed by two vectors, and is calculated as follows

$$\vec{a} \wedge \vec{b} = a_x b_y - a_y b_x $$

Now, let us see if this will appear anywhere while we explore the the equation of $\vec{n}$. Let's write it as follows:

$$\vec{n} = \alpha \vec{u} + \beta \vec{v} $$

where $\alpha$ and $\beta$ are Rational Numbers acting as Scalars for the vectors $\vec{u}$ and $\vec{v}$. Now split it into components.

$$n_x = \alpha u_x + \beta v_x \tag{1}$$ $$n_y = \alpha u_y + \beta v_y \tag{2}$$

Now we can solve the system of two equations with two unknowns, for alpha ($\alpha$) and beta ($\beta$). There are many ways to do this but let us try the following method: Multiply equation 1 by $u_y$ and equation 2 by $u_x$ and we get this:

$$u_y n_x = \alpha u_x u_y + \beta u_y v_x \tag{1a}$$ $$u_x n_y = \alpha u_y u_x + \beta u_x v_y \tag{2a}$$

Now subtract equation 2a from equation 1a

$$ u_y n_x - u_x n_y = \beta ( u_y v_x - v_x u_x ) $$

Notice that $u_y n_x - u_x n_y$ is the Wedge Product of $\vec{n}$ and $\vec{u}$, or in math notation, $\vec{n} \wedge \vec{u} = u_y n_x - u_x n_y$. The same for v and u on the right hand side. We can rewrite the equation for $\beta$ as follows:

$$ \beta = \frac{ \vec{n} \wedge \vec{u}}{ \vec{v} \wedge \vec{u} } $$

If we follow a similar procedure we can solve for alpha

$$ \alpha = \frac{ \vec{n} \wedge \vec{v}}{ \vec{u} \wedge \vec{v} } $$

We shall come back to this later.

Modular Arithmetic on Scalars

Now let's take a new road, and imagine if we introduce modular arithmetic to our rational scalars $\alpha$ and $\beta$ here?

Remember our first equation for $\vec{n}$, with Rational Numbers $\alpha$ and $\beta$

$$\vec{n} = \alpha \vec{u} + \beta \vec{v} $$

Let's change it to highlight the rational nature of $\alpha$ and $\beta$, by saying $\alpha_{num}$ is the numerator of $\alpha$ and $\alpha_{den}$ is the denominator of $\alpha$

$$\vec{n} = \frac{\alpha_{num}}{\alpha_{den}} \vec{u} + \frac{\beta_{num}}{\beta_{den}} \vec{v} $$

Now lets bring in a little computer math. In computer programs it can be common to use integer-rounding division and modular division together to deal with fixed width buffers like pixel screens. Let's try something a little similar here.

Notice that for any rational $\frac{a}{b}$ we can re-write this as follows (where $\small{a \mod\ b}$ is the Modulo division operator, in most computer languages represented as a%b, signifying the remainder of integer division).

$$\frac{a}{b} = \lfloor \frac{a}{b} \rfloor + \frac{a \mod b}{b}$$

For example

$$\frac{7}{3} = \lfloor \frac{7}{3} \rfloor + \frac{ 7 \mod 3 }{3}$$ $$\frac{7}{3} = 2 + \frac{1}{3}$$

We can do the same with $\frac{\alpha_{num}}{\alpha_{den}}$

$$\frac{\alpha_{num}}{\alpha_{den}} = \lfloor \frac{\alpha_{num}}{\alpha_{den}} \rfloor + \frac{\alpha_{num} \mod \alpha_{den}}{\alpha_{den}}$$

Let's rename the terms to be a little easier to write and introduce $\alpha_q$ and $\alpha_r$

$$\alpha = \frac{\alpha_{num}}{\alpha_{den}} = \alpha_q + \alpha_r$$ where $$\alpha_q = \lfloor \frac{\alpha_{num}}{\alpha_{den}} \rfloor$$ $$\alpha_r = \frac{\alpha_{num} \mod \alpha_{den}}{\alpha_{den}}$$

What if do the same for beta, and then we plug that back into our equation for $\vec{n}$?

$$ \vec{n} = \alpha \vec{u} + \beta \vec{v} = ( \alpha_q + \alpha_r ) \vec{u} + ( \beta_q + \beta_r ) \vec{v} $$

We can distribute the alphas and betas

$$ \vec{n} = \alpha_q \vec{u} + \alpha_r \vec{u} + \beta_q \vec{v} + \beta_r \vec{v} $$

Now we can begin to see where $\vec{d}Q$ and $\vec{r}$ come from in this vector and wedge view of this world. Recall the original equation - we can equate the $\vec{d}Q$ and $\vec{r}$ to terms in our new written equation, as follows:

$$\vec{n} = \vec{d}Q+\vec{r}$$

$$\vec{d}Q = \alpha_q \vec{u} + \beta_q \vec{v} $$

$$\vec{r} = \alpha_r \vec{u} + \beta_r \vec{v} $$

Put it together

Given $\vec{u}, \vec{v}, \vec{n},$ where $\vec{n} = \vec{d}Q+\vec{r}$, we can calculate $\vec{d}Q$ and $\vec{r}$ as follows

$$\alpha_{num} = \vec{n} \wedge \vec{v}$$ $$\alpha_{den} = \vec{u} \wedge \vec{v}$$ $$\alpha = \frac{\alpha_{num}}{\alpha_{den}} $$ $$\alpha_q = \lfloor \frac{\alpha_{num}}{\alpha_{den}} \rfloor$$ $$\alpha_r = \frac{\alpha_{num} \mod \alpha_{den}}{\alpha_{den}} $$

Follow the same pattern for $\beta$. Then

$$\vec{d}Q = \lfloor \frac{\alpha_{num}}{\alpha_{den}} \rfloor \vec{u} + \lfloor \frac{\beta_{num}}{\beta_{den}} \rfloor \vec{v} $$ $$\vec{r} = \frac{\alpha_{num} \mod \alpha_{den}}{\alpha_{den}} \vec{u} + \frac{\beta_{num} \mod \beta_{den}}{\beta_{den}} \vec{v} $$

If you want to write out all the wedges, we can say this:

$$\vec{d}Q = \lfloor \frac{\vec{n} \wedge \vec{v}} {\vec{u} \wedge \vec{v}} \rfloor \vec{u} + \lfloor \frac{\vec{n} \wedge \vec{u}} {\vec{v} \wedge \vec{u}} \rfloor \vec{v} $$

$$\vec{r} = \frac{\vec{n} \wedge \vec{v} \mod \vec{u} \wedge \vec{v} }{\vec{u} \wedge \vec{v}} \vec{u} + \frac{\vec{n} \wedge \vec{u} \mod \vec{v} \wedge \vec{u} }{\vec{v} \wedge \vec{u}} \vec{v} $$

Example Calculations

Perhaps it is useful to note that the Wedge product is the signed area of a parallelogram formed by the two given vectors, so $\vec{u} \wedge \vec{v}$ is simply the negative of $\vec{v} \wedge \vec{u}$ In theory, then, the calculation for d and r could be done with only three wedge-products.

Let's do the basic example

$$ \vec{n} = (3,5), \vec{u} = (2,1), \vec{v} = (-1,2) $$

$$ \vec{n} \wedge \vec{v} = 6--5 = 11 $$ $$ \vec{n} \wedge \vec{u} = 3-10 = -7 $$ $$ \vec{u} \wedge \vec{v} = 4--1 = 5 $$ $$ \vec{v} \wedge \vec{u} = -5 $$

$$ \vec{d}Q = \lfloor \frac{ 11 }{ 5 } \rfloor (2,1) +\lfloor \frac{-7}{-5} \rfloor (-1,2) $$ $$ = (4,2) + (-1,2) = (3,4) $$

$$\vec{r} = \frac{11 \mod 5}{5} (2,1) + \frac{-7\mod -5}{-5} (-1,2)$$

$$ = \frac{1}{5} ( 1(2,1)+2(-1,2) ) = \frac{1}{5}(0,5) = (0,1)$$

Which matches the example.

From this calculation we can see that the "red" grid locations on the original question also have a "remainder" $\vec{r}$ of $(0,1)$ , for example if we move to a different $\vec{n}$ of $(4,3)$:

$$ \vec{n} = (4,3), \vec{u} = (2,1), \vec{v} = (-1,2) $$ $$ \vec{n} \wedge \vec{v} = 8--3 = 11 $$ $$ \vec{n} \wedge \vec{u} = 4-6 = -2 $$ $$ \vec{u} \wedge \vec{v} = 4--1 = 5 $$ $$ \vec{v} \wedge \vec{u} = -5 $$

$$ \vec{d}Q = \lfloor \frac{ 11 }{ 5 } \rfloor (2,1) +\lfloor \frac{-2}{-5} \rfloor (-1,2) = 2(2,1)+0(-1,2)=(4,2) $$ $$ \vec{r} = \frac{11 \mod 5}{5} (2,1) + \frac{-2 \mod -5}{-5} (-1,2) $$ $$ = \frac{1}{5}(2,1) + \frac{-2}{-5}(-1,2) = \frac{1}{5} ( (2,1) + 2(-1,2) ) = (0,1) $$

If we change $\vec{v}$ so that $\vec{u}$ and $\vec{v}$ are no longer square (orthogonal) to each other, we get different values for $\vec{r}$.

For example, $\vec{u} = (2,1), \vec{v} = (1,3)$ results in the following possibilities for $\vec{r}$, which is $P$

$$P = {(0,0), (1,1), (1,2), (2,2), (2,3)}$$

If you draw these out, you will see they are roughly the pixels "inside" the parallelogram created by $\vec{u}=(1,2)$ and $\vec{v}=(1,3)$

Example pictures

Let's look at some pictures to see if this seems like it's working properly. We can do calculations per above, then draw the resulting $\vec{d}Q$s and $\vec{r}$s using python3 and easygraphics.

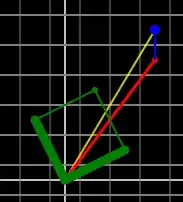
First let's replicate the original question picture using this algorithm. $\vec{u}$ and $\vec{v}$ are big green, with u+v extended by small green lines, to show the extent of the parallelogram formed by u and v. $\vec{d}Q$ is red, $\vec{r}$ is blue, and $\vec{n}$ is yellow.

Now let us replicate this but we will try sixteen different values for $\vec{n}$, in a grid from 1,1 to 4,4. $\vec{n}$s are omitted for clarity. This seems to be matching the grid patterns in the original question:

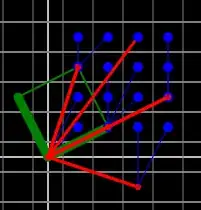
If we gather all the values of $\vec{r}$s calculated here, we get $P$, and we can also draw it's values:

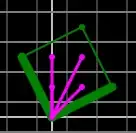
These are all inside the parallelogram formed by $\vec{u}$ and $\vec{v}$ and match the original picture.

---

The next image is the same but with $\vec{u} = (-4,2)$ and $\vec{v} = (1,2)$ and $\vec{n}$ ranging from x = -5 to 1 and y = 0 to 5. The Ps have been drawn in Magenta on top of the r's, and d's.

---

Now, does it work for "non square" or "not right angle" choices of u and v? (where $\vec{u}$ is not orthogonal to $\vec{v}$). This picture seems to show that it works reasonably well.

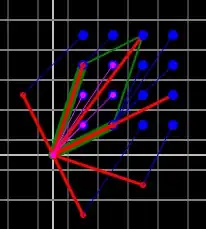
It even seems to work pretty well for $\vec{u}$ and $\vec{v}$ in the third quadrant, when all xs and ys are negative.

Tiling of the plane

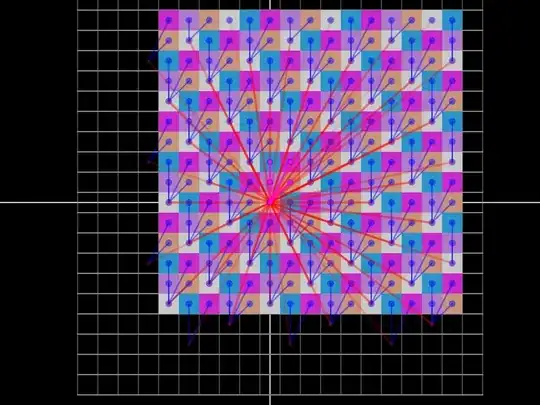
Turns out these also create tilings of the plane, using a sort of pixellated parallelogram.

With each $\vec{r}$ given it's own color, we get a picture kind of like the first picture in the question

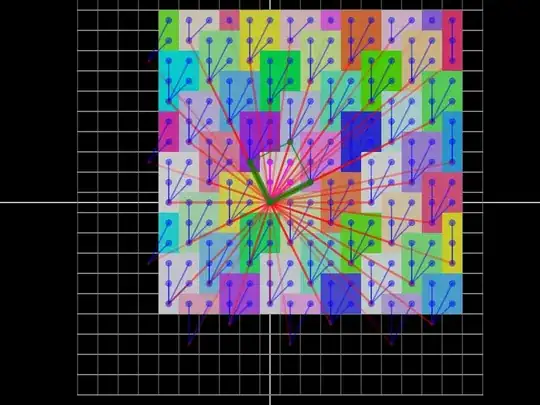
If we make the coloring based on $\vec{d}Q$ we get a covering of Polyominoes

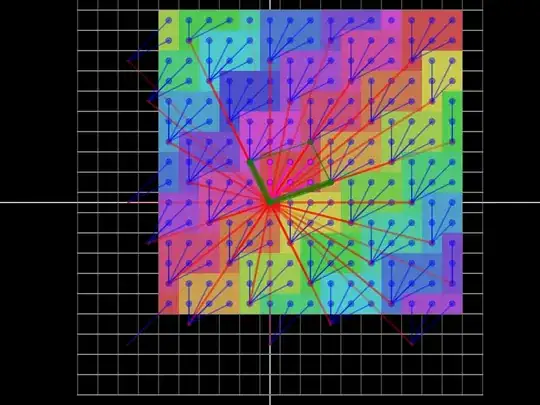
... and a different choice of $\vec{u}$ and $\vec{v}$ gives a different Polyominoe...

As for the hexagonal grid, I am not sure how to do the same there.

And I am not so sure about modular n, it seems to me like any two vectors $\vec{n_1}$ and $\vec{n_2}$ are "congruent" if they both have the same $\vec{r}$. But I'm not sure how to express it.

Hopefully this is a partial answer to the original question.