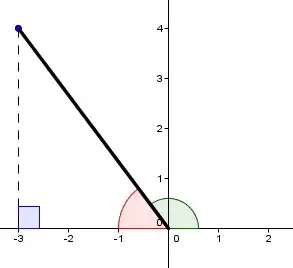
So I have a rough idea on how to get the answer but I'm getting stuck on the angle or argument for the equation. The question is:
Find the 6th root of $-3+4i$.
I first find the $r$ value which is 5, now I need to find the angle that connects them and I'm told I need to plug $\tan(\frac ba)$ and that would give me $\tan(-\frac {4}{3}) $.
My teacher had mentioned using $\arctan$ to get the correct angle but I can't remember the process.