2

I'm stuck on Exercise 5.2.1 of Goldblatt's "Topoi: A Categorial Analysis of Logic":

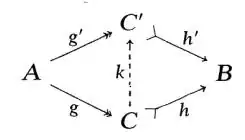
Given a function $f:A\to B$, if $h\circ g: A\twoheadrightarrow C\rightarrowtail B$ and $h'\circ g': A\twoheadrightarrow C'\rightarrowtail B$ are two different epic-monic factorisations of $f$ (i.e. $f=h\circ g=h'\circ g'$), then there exists a unique $k:C\to C'$ such that

enter image description here

commutes, and furthermore $k$ is iso in $\mathbf{Set}$.

The rest of the section seems okay. It gives a categorical proof in any topos. However, I'd like a set-theoretic proof please.

I've tried defining $k: C\to C'$ by way of equivalence classes; namely, by letting $k(c)=g'(\gamma)$ for some $\gamma$ with $c=g(\gamma)$, so that since $g$ in onto, I can iron out any ambiguity by saying $\gamma\sim_{g}\delta$ iff $g(\gamma)=g(\delta)$, then go from there. (Do you see what I mean?) I can't get it to work.

Please help :)

Community
  • 1
Shaun
  • 44,997

2 Answers2

2

I would use the context of binary relations for a clear proof.

Let $r$ be a relation between $A$ and $B$, i.e. $r\subseteq A\times B$ (or $r:A\times B\to\{false,\ true\}$ if you prefer), and let $\def\inv{^\smallsmile} r\inv$ denote the inverse relation $\subseteq B\times A$. Using infix notation, it means that $$a\mathop rb\iff b\mathop{r\inv}a\,.$$ Also, define $r\le r'$ iff $r\subseteq r'$ as sets, i.e. $r(a,b)\Rightarrow r'(a,b)$ for all $a\in A,\,b\in B$.

Let me write composition of relations from left to right and $1_A$ for the equality relation on set $A$.

Verify that for a relation $f\subseteq A\times B$ we have that

  1. $f$ is a 'partial function' ($a\mathop fb,\,a\mathop fb'\implies b=b'$)$\,$ iff $\ f\inv f\le 1_B$
  2. $f$ is 'everywhere defined'$\,$ iff $\ ff\inv\ge 1_A$
  3. $f$ is 'injective' iff $\ f\inv$ is a partial function, i.e. $\ ff\inv\le 1_A$
  4. $f$ is 'surjective' iff $\ f\inv$ is everywhere defined, i.e. $\ f\inv f\ge 1_B$.

Thus in our situation, we have $g\inv g=1_C=hh\inv$ and the same way, $g_1\inv g_1=1_{C'}=h_1h_1\inv$.

Now $k:=g\inv g_1$. This also equals to $hh_1\inv$ because $g\inv g_1h_1=g\inv f=g\inv gh=h $, so
$g\inv g_1=g\inv g_1h_1h_1\inv=h\,h_1\inv$.

Finally, $k\inv=g_1\inv g$ and we can easily check that $kk\inv=1_C$, and by the same argument, $k\inv k=1_{C'}$, which proves that $k$ is a bijection.

Berci
  • 90,745
1

Since $h'$ is injective, the inverse $(h')^{-1}$ is well-defined on $f(A) = h'(C')$.

Therefore we can set $k = (h')^{-1}\circ h$.

Daniel Fischer
  • 206,697
Shaun
  • 44,997
  • What is the purpose of this "answer"? – Martin Brandenburg Jun 23 '14 at 13:01
  • 1
    @MartinBrandenburg I read in the meta site that if a question is answered in the comments, then it's acceptable to say so in a community wiki answer (which is then accepted). It takes it off the list of unanswered questions :) – Shaun Jun 23 '14 at 13:05
  • @MartinBrandenburg I welcome more answers (of course). I suppose it would have been better to ask Daniel Fischer to post the answer himself too. I'll do that next time :) – Shaun Jun 23 '14 at 13:10
  • @MartinBrandenburg The purpose of the set-theoretic answer is to contrast it with the categorical one under the advice Goldblatt :) – Shaun Jun 23 '14 at 13:16