The following method is elementary, but perhaps not very elegant. (Hopefully others will find a more beautiful solution.)
(NB: Each of the figures can be clicked on to display a larger version.)
Before we begin, first note that the absolute relative error of $\sqrt{2} + \sqrt{3}$ with respect to $\pi$ is quite small. Indeed,
$$
\left|\frac{\sqrt{2}+\sqrt{3} - \pi}{\pi}\right| < 0.0015 = 0.15\% \,,
$$
so it would seem that any geometric construction would have to be pretty precise.
Our solution is formed by constructing 16 adjacent (nonoverlapping) right triangles. Eight of these triangles have area $\sqrt{2}/64$ each and the other eight triangles are of area $\sqrt{3}/64$. The construction is done in such a way that, collectively, they are larger than 1/8 of a unit circle.
Below is the final picture followed by a discussion.
Final result
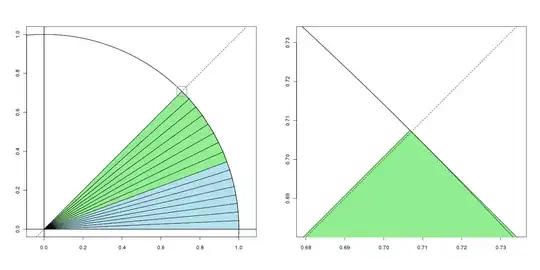
The triangles in blue are each of area $\sqrt{2}/64$ and each green one has area $\sqrt{3}/64$. The dotted line is the forty-five degree line, so that the portion of the circle between it and the $x$-axis is one-eighth of the whole and so has area $\pi/8$.
The right panel is a zoomed in version of the left panel. The small grey square on the forty-five degree in the left panel shows the "zoom" box that corresponds to the entire figure in the right panel.
Constructing tangent lines of length $\sqrt{2}$ and $\sqrt{3}$
To construct the necessary triangles, we need to be able to construct tangent lines to the unit circle of length $\sqrt{2}$ and $\sqrt{3}$, respectively.
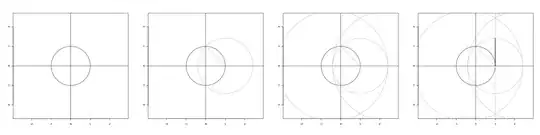
Below is one such construction of a line segment of length $\sqrt{2}$.
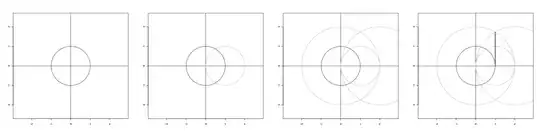
Here is a construction of a line segment of length $\sqrt{3}$.
Note that once we have a line segment of length $L$, it is straightforward to subdivide it to create segments of length $2^{-n} L$ for any nonnegative integer $n$.
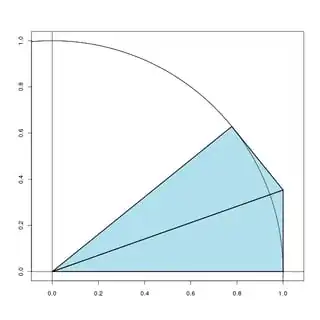
Example construction of paired right triangles
We form the right triangles in reflected pairs so that they always dominate the corresponding segment of the circle. Here is an example of a construction using a side length of $\sqrt{2}/4$ tangent to the unit circle. The two triangles put together obviously have area $\sqrt{2}/4$ in this example.
Final construction
To get the final construction, we use side lengths of $\sqrt{2}/32$ and $\sqrt{3}/32$, respectively. Constructing four adjacent pairs each of such triangles, we can strictly dominate one-eighth of a circle, hence
$$
\frac{\sqrt{2}}{8} + \frac{\sqrt{3}}{8} > \frac{\pi}{8}
$$
which is clearly equivalent to the desired inequality.



