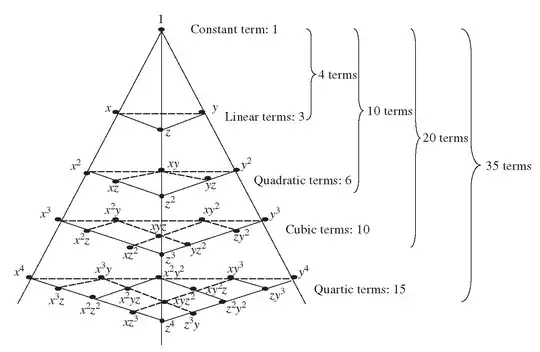
(hope it doesn't seem so weird), I'm looking for a general expanded form of $(x+y+z)^k, k\in\mathbb{N}$.
$k=1: x+y+z$
$k=2: x^2+y^2+z^2+2xy+2xz+2yz$
$k=3: x^3+y^3+z^3+3xy^2+3xz^2+3yz^2+3x^2y+3x^2z+3y^2z+6xyz$
$k=4: x^4+y^4+z^4+4xy^3+4x^3y+4xz^3+4x^3z+4yz^3 +4y^3z+6x^2y^2+6y^2z^2+6x^2z^2+12x^2yz+12xy^2z+12xyz^2$
The elements are obviously determined by combinations of their powers, whose sum is always $k$. I just cannot find the algorithm for element's constants