how to see the logarithm as the inverse function of the exponential?

Question

I saw here in math.stackexchange some proofs of how the log and exp functions are related to each other, but I want to get an intuition for that.

In layman terms, how would you explain the connection between these 2 functions?

Answer 1

You want to understand that exponential and logarithms are inverse of each other:

(i)$ f(x) = y$, if we want to find the inverse, we express $x$ in terms of $y$. I will show you graphically.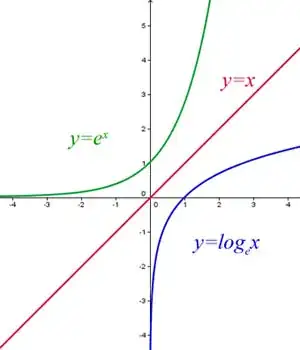. (This is equally applicable for other exponents)

Which is one way of seeing that both are inverse of each other.

(ii) $a > 0$ and $x > 0$, condition $a \ne 1$, the logarithm base $a$ of $x$,

we write $\log_a(x)$, which is the exponent to which $a$ to be raised to obtain $y$. $\log_a(x) = y$, which is same as $a^y = x$. The functions $\log_a(x)$ and $a^x$ are clearly inverses of each other. The domain of logarithm base $a$ is all positive numbers and range is all real numbers.

Using the fact that the domain and range of any invertible function are just the range and domain of its inverse.

Here, the domain $\rightarrow$ logarithm base $a$ function is the range $\rightarrow$ $a^x$ function (remember for all positive no.)

and the range $\rightarrow$ logarithm base $a$ function is the domain $\rightarrow$ $a^x$ function (here it is for all numbers).

Answer 2

A simple way to state how they're related would be that one function will undo the other.

$$\log(e^x)=x$$ $$e^{\log x}=x$$

Answer 3

For a positive real number $\;a\neq 1\;$, we have by definition

$$a^y=x\iff \log_ax=y\;,\;\;x>0$$

In words: the logarithm in base $\;a\;$ of a positive number $\;x\;$ is the exponent to which the base must be raised in order to get $\;x\;$ .

Thus, for example, $\;\log_381=4\;$ since the base $\;3\;$ must be raised to the fourth power in order to get $\;81\;$.

Once one swallows and assimilates this, the tight relation between logarithms and exponentials becomes much clearer. For example:

$$\begin{cases}&\log_3x=y&\iff 3^y=x\\{}\\ &3^y=x&\iff \log_3x=y\end{cases}$$

and from this is now clear that $\;f(x):=\log_ax\;,\;\;g(x):=a^x\;$ are inverse functions to each other, meaning:

$$f\circ g(x)=f(g(x))=\log_a(a^x)=x=3^{\log_ax}=g(f(x))=g\circ f(x)$$

Answer 4

If purely for a layman discussion I would go with integers and the $log_{10}$ route.

The number 981 is 3 digits so $log_{10}981$ is close to 3. If you do $10^3$, or $exp(3)$ you get a number close to 981; $exp(3)$ is of the same magnitude as $981$.

In this context the usefulness, in my opinion, would be to use $log$ to describe a magnitude, and also an intuitive way to understand exponential growth. In each step of exponential growth you add one* more digit.

*or whatever the growth rate may be.

Answer 5

Consider first for any positive fixed $x$ : $$\tag{1} y_t:=\int_1^x z^{t-1}\,dz=\frac {x^t-1}t$$ then (see too this discussion) : $$\tag{2}y_0=\lim_{t\to 0}\int_1^x z^{t-1}\,dz=\lim_{t\to 0}\frac {e^{t\log(x)}-1}t=\log(x)$$ But $(1)$ may be reversed to get : $$\tag{3}x=\left(1+t\;y_t\right)^{1/t}$$ and again as $\,t\to 0$ we get the usual $$\tag{4}x=e^{\,y_{\,0}}$$ that is the wished converse of $(2)$.

Hoping this will give some intuition too,

Answer 6

Specifically, if $a=e$, then $\ln b =c$ if and only if $e^c=b$.

Answer 7

By definition. That's how I learned it in high school.

The teacher started class with something like $2^y=x$ and asked us to solve for $y$. Nobody could do it. Then she said "define this thing called a logarithm such that $\operatorname{log}_{base}(\mathrm{answer})=\mathrm{exponent}$" and gave us the mnemonic "b ase a nswer e xponent" to remember it. I still use "bax" once in a while.

All the other properties came out of "well, it turns out that when you define a log this way you get such and such properties" like the multiplication rules, which we then spent the next few classes proving.

Answer 8

For the layman it might help to know that logarithms were used as a tool for multiplication back when ships sailed by celestial navigation. The sum of the logarithms of two numbers is the logarithm of their product. Extensive log tables were published and used by rote. This made a nice extra topic for 6 grade math in 1958. Our teacher gave no hint of a link to integrals, but the relation to exponents was taught.

As a physical correlate, the slide rule uses one axis graphs of an exponential function to convert multiplication to addition of lengths, a graphic log table.

Answer 9

You could point out their opposite algebraic properties.

For logarithms you have the product rule:

$$ \log(a b) = \log(a) + \log(b) $$

So the logarithm of a product is the sum of the logarithms of its factors.

For exponential functions you have the opposite relationship:

$$ \exp(a + b) = \exp(a) \exp(b) $$

So the exponent of a sum is the product of the exponents of its summands.

If we chose the $\log$ function accordingly so that $\log(e)=1$ and note that $\exp(x)=e^x$ it's easy to see that these properties imply the inverse function relationship, since the two rules give us

$$ \log(\exp(x)) = x \log(e) = x $$

(At least that should be clear when $x$ is an integer, but it also works with rationals. For real numbers you probably have to show cauchy convergence but I guess that would not be necessary for a layman.) Note that this doesn't imply that $e$ is Euler's number, but I think this doesn't matter for your question, since the inverse relationship is valid for any base. Probably more important is that there are existing two such functions for any $e\not=0$.