Every polygon has an interior diagonal

Question

How does one prove that in every polygon (with at least 4 sides, not necessarily convex), that it is possible to draw a segment from one vertex to another that lies entirely inside the polygon.

In particular, I'm having trouble rigorously defining the "inside of polygon." For a convex polygon, one can define the inside as the union of half-planes that are extensions of the sides. However, I'm not sure how to do this for the non-convex polygons.

I'd like to do this rigorously, considering the polygon as a figure in $\mathbb{R}^2$, instead of appealing to geometric intuition.

Edit: obviously, I need to specify nonintersecting.

Answer 1

I will just attend to the question of inside/outside. It follows from the Jordan Curve Theorem that your polygon splits the plane into two parts, an inside and an (unbounded) outside. To get from one to the other, we insist on smooth curves (or, for that matter, polygonal paths) that cross the polygon only once, not at a vertex, and at a nonzero angle to the segment crossed (tangency not allowed).

As a result, the simple test for inside/outside, for extremely convoluted figures, is to start a some point very far from the polygon, draw a path to the point of interest, and count the number of times the path crosses the polygon (permitting only the types of crossing indicated above). If the number of crossings is $0$ or otherwise even, the point of interest is outside the polygon. If the number of crossings is $1$ or otherwise odd, the point of interest is inside the polygon.

EDIT **** SATURDAY: A very good proof and discussion is given by Joseph O'Rourke, website OROURKE in Chapter One of his book Art Gallery Theorems and Algorithms, which one may download as separate chapters. In Chapter One, "Polygon Partitions," page 12, there is a quick proof for your question, as part of Theorem 1.2. Take three consecutive vertices $v_1, v_2, v_3$ such that the angle is "convex" with regard to the polygon $P$, that is, a tiny neighborhood of $v_2$ inside the angle $v_1 v_2 v_3$ (demanded below $\pi$) is also inside the polygon $P.$
          
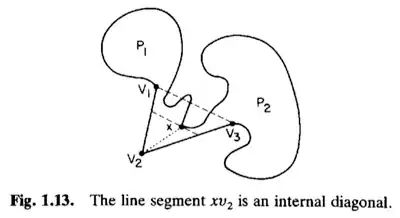
Perhaps $v_1 v_3$ is a line segment completely contained in $P,$ in which case we are done. If not, it means there are other vertices of the original polygon inside the triangle with vertices $v_1, v_2, v_3.$ Find the vertex, call it $x,$ that is inside the triangle and is closest to $v_2,$ distance measured only in the direction perpendicular to segment $v_1 v_3$ (see Figure 1.13). As a result, the line through $x$ and parallel to $v_1 v_3$ can not intersect any other edges of $P$ inside the triangle $v_1 v_2 v_3.$ Then the segment $v_2 x$ is completely inside $P.$ . Note that measuring distance for $x$ by full Euclidean distance may not work properly here. Draw some pictures! On page 13, he mentions Meister's Two Ears Theorem (1975), Theorem 1.3, which is probably the item you saw quoted.

Evidently Meister is G. Meister, "Polygons have ears," American Mathematical Monthly, volume 82, pages 648-651, 1975.

O'Rourke:

https://math.stackexchange.com/users/237/joseph-orourke

https://mathoverflow.net/users/6094/joseph-orourke

Answer 2

This is not entirely rigorous but I suspect it can made such. Suppose that our polygon is not convex. Then there is some vertex $v_i$ at which the interior angle is over $\pi$. Consider rotating the ray going through points $v_i,v_{i-1}$ to the ray going through points $v_i,v_{i+1}$ through the interior of the polygon. Now consider the point at which this ray first hits the boundary of the polygon. This gives us a piecewise continuous function $f \colon (0,\alpha) \to \partial P$ where $\alpha$ is the interior angle at $v_i$. Moreover the continuous pieces are line segments. We have to prove that there is a vertex in the image of $f$. Assume there was not. Then $f(0,\alpha)$ would be a line segment from $v_{i-1}$ to $v_{i+1}$. But this is a contradiction because of the way $v_i$ was chosen.

Answer 3

Existence of an interior diagonal is equivalent to the ability to triangulate polygons (that are free of self-intersections).

Some algorithms are described at wikipedia:

http://en.wikipedia.org/wiki/Polygon_triangulation

Answer 4

In order to prove what is called the Bolyai-Gerwien-Wallace Theorem, that if one has two plane simple polygons of the same area then one can cut the first polygon into a finite number of simple polygons and reassemble the pieces (jigsaw puzzle style) into the other polygon, Larwrence Levy in the book Geomety: Modern Mathematics via the Euclidean plane (Prindle, Weber & Schmidt, 1970) first gives a proof (p. 142-143) that any plane simple polygon can be triangulated using the fact (with proof) that one can find two vertices (not ends of an edge) of a simple polygon which can be joined by a line segment lying (except for its ends) totally in the interior of the polygon.

Answer 5

There is a detailed completely arithmetic proof on pp 103-107 in Estermann's text "Complex Numbers and Functions," Athlone Press, 1962.