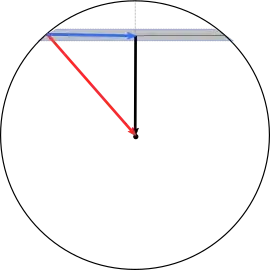
Imagine a spherical airless body. It is small enough that central pressure allows a tunnel to be built from north pole to the south pole. I jump in the tunnel at the north pole and fall to the south pole. How long would it take me? What I believe to be the correct answer is the period of a circular orbit having the planet's radius, r. If I remember correctly, I heard this argument from Dr. John Stockton:
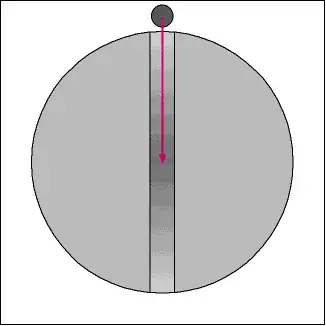
Break the acceleration vector of the orbiting body into orthogonal components. The orbiting body's acceleration vector would have the same north/south component as the object bobbing up and down the mohole. So the period of the bobbing object would be $2\pi \sqrt{r^3/\mu }$
But how long would it take for a subway car to roll from one end of the chord to the other if the chord doesn't pass through the body's center?
I'm imagining a science fiction setting where 12 subway stations are built on the surface of Ceres, each station corresponding to the vertices of an icosohedron.
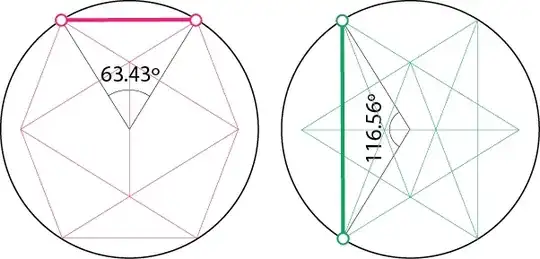
Tunnels linking stations to their nearest neighbors are chords subtending 63.43º. These tunnels from the edges of an icosohedron.
Tunnels linking stations to their second nearest neighbors are chords subtending 116.56º. These tunnels form the edges of a small stellated dodecahedron.
And of course there'd be 6 tunnels linking stations 180º from one another. I think I have handle on these.
For the moment I'm not considering friction or the so called centrifugal force a spinning Ceres would induce.