Complex integration Question - Contour Method

Question

I'm asked to find:

$$\int_{-\infty}^\infty \frac{\ln(x^2+1)}{1+x^2} dx $$

Attempt

Considering $$ \oint \frac{\ln(z^2+1)}{(z+i)(z-i)} dz $$

So first I find the branch points of the function.

This function has a simple pole at $z=i$ and an essential singularity at $z=-i$.

Using this contour:

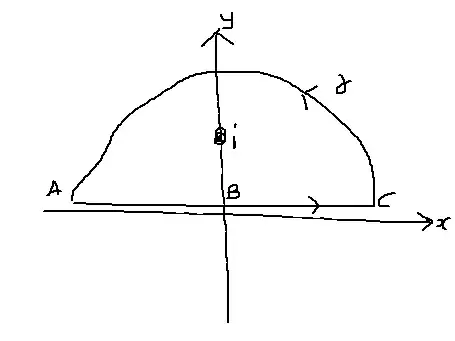
By residue theorem,

$$\int_\gamma + \int_AB + \int_BC = 2\pi i \times \text{Residue} $$

$$ \text{Residue} = \frac{\ln(2i)}{2i} = \frac{\pi}{4} - \frac{i}{2}\ln(2) $$

Taking the semi-circle to infinity, $\int_\gamma \rightarrow 0$ by Jordan's Lemma.

$$\int_{-\infty}^0 \frac{\ln(-|x| + i)}{1+x^2} dx + \int_0^{\infty} \frac{\ln(x+i)}{1+x^2} dx = 2\pi i \left[ \frac{\pi}{4} - \frac{i}{2}\ln(2) \right] $$

$$ \int_{-\infty}^0 \frac{\ln (i - |x|) + i\pi}{1+x^2} dx + \int_0^{\infty} \frac{\ln(x+i)}{1+x^2} dx = 2\pi i \left[ \frac{\pi}{4} - \frac{i}{2}\ln(2) \right] $$

$$ \int_{\infty}^0 \frac{\ln (i - x) + i\pi}{1+x^2} dx + \int_0^{\infty} \frac{\ln(x+i)}{1+x^2} dx = 2\pi i \left[ \frac{\pi}{4} - \frac{i}{2}\ln(2) \right] $$

I have a hunch that the first integral must become $+\int_0^{\infty}$ for it to combine with the second integral to give $\int_0^\infty \frac{\ln(1+x^2)}{1+x^2}\,dx$ then we take the real part on the right. But I can't seem to show this..

Answer 1

$$\begin{eqnarray*}I=\int_{-\infty}^{+\infty}\frac{\log(1+x^2)}{1+x^2}\,dx &=& 2\int_{0}^{+\infty}\frac{\log(\cosh u)}{\cosh u}du=2\int_{1}^{+\infty}\frac{\log y}{y\sqrt{y^2-1}}dx\\&=&-2\int_{0}^{1}\frac{\log z}{\sqrt{1-z^2}}dz = -2\int_{0}^{\pi/2}\log\sin\theta\,d\theta\end{eqnarray*}$$ is a well-known integral, also treated here: Evaluating $\int_0^{\infty}\frac{\ln(x^2+1)}{x^2+1}dx$.