Please have a look at the function: $$f(x) = \left(x + \frac{1}{x^x}\right)^x - x^x$$
You may see the plot on Wolfram Alpha.
Why does it have such a weird behaviour from $x = 13$? It starts swinging up and down so weirdly!
Please have a look at the function: $$f(x) = \left(x + \frac{1}{x^x}\right)^x - x^x$$
You may see the plot on Wolfram Alpha.
Why does it have such a weird behaviour from $x = 13$? It starts swinging up and down so weirdly!
Using the binomial theorem, we get $$ \begin{align} \left(x+\frac1{x^x}\right)^x-x^x &=x^x\left[\left(1+\frac1{x^{x+1}}\right)^x-1\right]\\ &=x^x\left[\frac1{x^x}+\frac{x-1}2\frac1{x^{2x+1}}+O\left(\frac1{x^{3x}}\right)\right]\\ &=1+\frac1{2x^x}+O\left(\frac1{x^{x+1}}\right) \end{align} $$ If you are getting wild oscillations or quantized output, it is probably due to truncation error.
The bottleneck actually seems to be in the computation of $x+\frac1{x^x}$ since IEEE double precision arithmetic only has a $53$ bit mantissa. $13$ has $4$ bits and $13^{-13}$ has $48$ zeros after the binary point before the first non-zero bit. So there is just barely enough precision to note that there is a difference between $x+\frac1{x^x}$ and $x$. Any imprecision in the computation would completely overwhelm this difference and cause extreme problems in the final computation.
As others have said this is a floating point error. If I plot it in mathematica I find:

Which clearly resembles the output by WolframAlpha (although they are not the same). If I increase the precision of the calculations and replot the same equation I find the following:
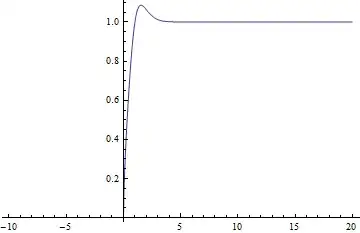
Note the change in scale.
Even with this increased precision you will still find erroneous weird behavior after some time and you will have to increase the working precision again (ad infinitum).
Yes, almost certainly floating point error.
$$f(x)= x^x\left(\left(1+\frac{1}{x^{x+1}}\right)^x-1\right)$$
For $x$ large, $\left(1+\frac{1}{x^{x+1}}\right)^x = 1+\frac{1}{x^x}+O(x^{-2x})$
So $f(x)=1+ O(x^{-x})$.
x ∈ (7, 8)? Why is the bouncing doesn't start abruptly, but increases so mildly? – soshial Jun 10 '14 at 17:59Plot[(x + 1/x^x)^x - x^x, {x, 1, 20}, WorkingPrecision -> 100, PlotRange -> All, Axes -> False, Frame -> True]produces this plot: http://i.stack.imgur.com/7lUmq.png – Antonio Vargas Jun 11 '14 at 02:50