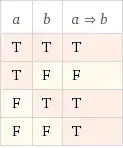
Suppose $x \in R^+$ and we want to prove the implication $x < 0 \Rightarrow P(x)$, where $P(x)$ is some statement of $x$.
How should one tackle this situtation ?
Normally one should prove the implication in the case that the antecedent is false and in the case that the antecedent is true, where the false case follows (is true) by definition.
Should one prove the implication in the case $x < 0$ (antecedent is true) even thus $x \in R^+$, or is the case optional (we can just say the truth case will never happen ?).
More generally suppose we don't know whether $P(x)$ can be true for any $x$, and we want to prove $P(x) \Rightarrow Q(x)$.
Is it then O.K to assume $P(x)$ is true if it is false for all values of $x$ ? Should one prove the implication for $P(x)$ assumed to be true in order to prove the implication ?