0

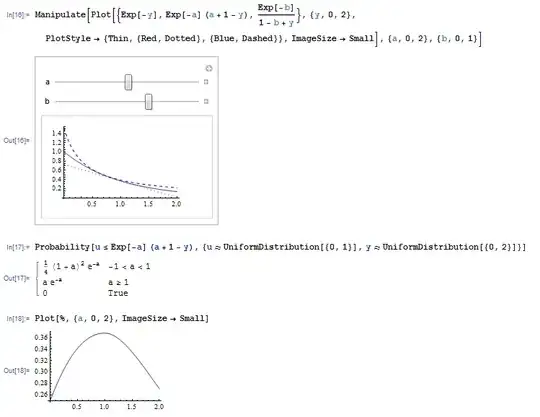
A variant method of squeezed rejection algorithm for the simulation of the exponential distribution $\exp(1)$ truncated to $(0,2)$ interval can be written as:

(a) generate $Y \sim U(0,2)$ , $U\sim U(0,1)$

(b) if $U \le \mathrm{e}^{-a} \times (a+1-Y)$ go to (e)

(c) if $U> \mathrm{e}^{-b}/(1-b+Y)$ go to (a)

(d) if $U> \mathrm{e}^{-Y}$ go to (a)

(e) set $X=Y$

Prove that the probability of success in step (b) is equal to $a \times \mathrm{e}^{-a}$ if $a\ge 1$ and equal to $1/4 \times (a+1)^2 \times \mathrm{e}^{-a}$ if $a<1$. Prove that the best choice is $a=1$

a,b>0 (a,b)εΝ

Panagiotis
  • 31

1 Answers1

1

Here are some hints:

  • Show that for all $0 < a < 2$, $0<b<1$ and $0<y<2$, $$ \mathrm{e}^{-a} (a-y+1) \leq \mathrm{e}^{-y} \leq \frac{\mathrm{e}^{-b}}{y+1-b} $$ To this end, use $1+x \le \exp(x)$, valid for all $x \in \mathbb{R}$. Change $x \to -x$, and restricting to $1-x > 0$, derive $\exp(x) \le\frac{1}{1-x}$.

  • Compute $\mathbb{P}( U \le \mathrm{e}^{-a} (a-Y+1))$. Notice that $F_U(u) = \mathbb{P}(U \le u) = \min(\max(u,0),1)$. Then use: $$ \begin{eqnarray} \mathbb{P}(U \le \mathrm{e}^{-a} (a-Y+1)) &=& \mathbb{E}( F_U(\mathrm{e}^{-a} (a-Y+1)) ) = \mathbb{E}(\min(\max( \mathrm{e}^{-a} (a-Y+1) ,0),1) ) \\ &=& \int_0^2 \min(\max( \mathrm{e}^{-a} (a-Y+1) ,0),1) \, \frac{1}{2} \mathrm{d}y \\ &=& \int_{0}^{\min(2,a+1)} \mathrm{e}^{-a} (a-Y+1) \frac{1}{2} \mathrm{d}y \end{eqnarray} $$

  • Finish the calculations, then maximize the function.

Here are some visual clues:

enter image description here

Sasha
  • 70,631
  • could you please explain what exactly are you doing here "To this end, use 1+x≤exp(x), valid for all x∈R. Change x→−x, and restricting to 1−x>0, derive exp(x)≤11−x." Thank you very much for your help the rest is quite understandalbe. – Panagiotis Nov 14 '11 at 00:28
  • @Panagiotis I meant replace in $1+y \le \exp(y)$, $y$ with $-x$, to get $1-x \le \exp(-x)$. Now, assuming $1-x > 0$, reciprocate and get $\frac{1}{1-x} \ge \frac{1}{\exp(-x)}$ which gives $\exp(x) \le \frac{1}{1-x}$. – Sasha Nov 14 '11 at 02:47
  • ok. i got it.again,thanks for your help. – Panagiotis Nov 14 '11 at 22:33