Given the Riemann-Siegel function, why are the Gram points important? I say if we have $S(T)$, the oscillating part of the zeros, then given a Gram point and the imaginary part of the zeros (under the Riemann Hypothesis), are the Gram points near the imaginary part of the Riemann zeros?
I say that if the difference $ |\gamma _{n}- g_{n} | $ is regulated by the imaginary part of the Riemann zeros.
One thing Gram points are good for is that they help in bracketing/locating the nontrivial zeroes of the Riemann $\zeta$ function.
More precisely, recall the Riemann-Siegel decomposition
$$\zeta\left(\frac12+it\right)=Z(t)\exp(-i\;\vartheta(t))$$
where $Z(t)$ and $\vartheta(t)$ are Riemann-Siegel functions.
$Z(t)$ is an important function for the task of finding nontrivial zeroes of the Riemann $\zeta$ function, in the course of of verifying the hypothesis. (See also this answer.)
That is to say, if some $t_k$ satisfies $Z(t_k)=0$, then $\zeta\left(\frac12+it_k\right)=0$.
Now, Gram points $\xi_k$ are numbers that satisfy the relation $\vartheta(\xi_k)=k\pi$ for some integer $k$. They come up in the context of "Gram's law", which states that $(-1)^k Z(\xi_k)$ tends to be positive. More crudely, we can say that Gram points tend to bracket the roots of the Riemann-Siegel function $Z(t)$ (i.e. there is often a root of $Z(t)$ in between consecutive $\xi_k$):
"Gram's law" doesn't always hold, however:
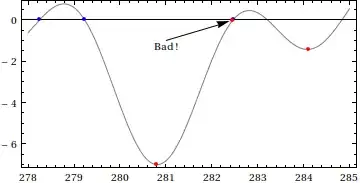
There are a number of other "bad" Gram points.
