The sharp bound is 14 for $n \geq 2$. That's the same as that for the Kuratowski problem, but the match appears to be a coincidence. For $n = 1$, the sharp bound is 4.
We'll focus on the $n \geq 2$ case. Denote $X = \mathbb R^n$. First, some preliminaries:
A cone is said to be a ray iff it has the form $\mathbb R_{>0} x = \{ ax : a>0 \}$ or $\mathbb R_{\geq 0} x = \{ ax : a \geq 0 \}$ for some $x \in X$. Rays of the first form are called blunt, while those of the second form are called pointed.
An open half-space is a set of the form $\{y \in X : \langle x, y \rangle > 0\}$ for some $x \in X$. More generally, we say that a convex cone $H$ is a half-space iff $O \subseteq H \subseteq O^-$ for some open half-space $O$. Note that $H^- = O^-$ is of the form $\{ y \in X : \langle x, y \rangle \geq 0\}$, and that $H^\circ = O$ ($\circ$ is the interior operation).
We show that the vector $x$ in the definition of a half-space is unique up to multiplication by a positive scalar for a given half-space $H$. Let $x_H \in H^\circ$ be a unit vector such that $H^\circ = \{y \in X : \langle x_H, y \rangle > 0\}$. Next, let $z \in X \setminus \mathbb{R}x_H$. Then $z^\bot := z - \langle x_H, z \rangle x_H$ is perpendicular to $x_H$, so $-z^\bot + \epsilon x_H \in H^\circ$ for all $\epsilon > 0$. Now
$$
\langle z, -z^\bot + \epsilon x_H \rangle
= -\langle z, z \rangle + \langle x_H, z \rangle^2 + \epsilon \langle x_H, z\rangle.
$$
Since $x_H$ and $z$ are not collinear, the Cauchy–Schwarz inequality tells us that $\langle x_H, z \rangle^2 < \langle x_H, x_H \rangle \langle z, z\rangle = \langle z, z \rangle$. Thus for sufficiently small $\epsilon$, we have $\langle z, -z^\bot + \epsilon x_H \rangle < 0$. Therefore $H^\circ \neq \{ y \in X : \langle z, y \rangle > 0\}$.
The above definitions and discussions imply that the dual of a ray is a closed half-space, and that the dual of a half-space is a pointed ray. In particular, for any half-space $H \subset X$, we have $H^* = \mathbb R_{\geq 0} x_H$ and $(\mathbb R_{>0}x_H)^* = (\mathbb R_{\geq 0}x_H)^* = H^-$.
So we distinguish two cases for your question.
Case 1. The starting cone $K$ is either a half-space, a ray, or one of $\varnothing$, $\{0\}$, and $X$.
If $K$ is a half-space, set $H = K$. Or if $K$ is a ray, let $x$ be the unit vector determining $K$. Then $x = x_H$ for some half-space $H$. The sets that can be generated are shown in the following diagram, in which $A \to B$ means $A^* = B$, and $A \dashrightarrow B$ means $A^c = B$.
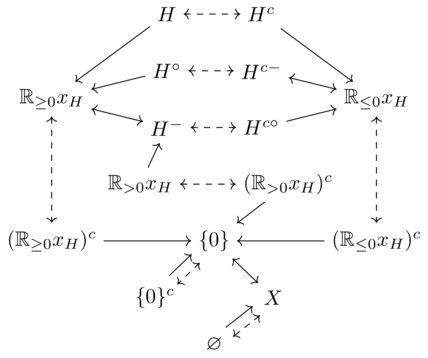
One can reach at most 14 nodes from any given starting point. A blunt ray is an example of a starting cone where all 14 nodes represent distinct sets.
Case 2. $K$ is none of the above.
Since $K \neq X$, the supporting hyperplane theorem tells us that $K$ lies in some half-space $H$. Moreover, we have that $K^\circ = K^{-\circ}$ (Corollary 1.2.12 here; also mentioned in another question), so $K^- \not\supseteq H^\circ$ (otherwise $K$ would be a half-space). It follows that $K^{c*} = K^{-c*} = \{0\}$.
What's more, $K^* \neq X$ is also not a half-space (otherwise $K^- = K^{**}$ would be a ray, hence $K$ would also be a ray). The same argument as above shows that $K^{*c*} = \{0\}$.
So we have a considerably simpler diagram, with only 10 nodes:
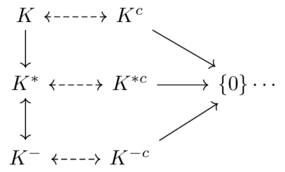
We are done.
I'll briefly mention the situation for other dimensions:
In $\mathbb R$, there are only 7 convex cones. The collections $\{\mathbb R_{<0}, \mathbb R_{\leq 0}, \mathbb R_{\geq 0}, \mathbb R_{>0}\}$ and $\{\varnothing, \{0\}, \{0\}^c, \mathbb R\}$ are each closed under the two operations and together contain the convex cones.
The situation where $X$ is an infinite-dimensional real Hilbert space is reasonably similar to that of $X = \mathbb R^n$, $n \geq 2$. Case 1 would be exactly the same. However, Case 2 would not: The supporting hyperplane theorem as stated for $\mathbb R^n$ no longer holds. Perhaps a weakened version of the supporting hyperplane theorem, that either $K$ is contained in a half-space or is dense, might still be true. We also have instances where $K$ is not a half-space but $K^-$ is (consider the algebraic linear span of an orthonormal basis, intersected with a half-space), but that just means that we would have a third case where we combine parts of the two diagrams, which isn't a big deal.

