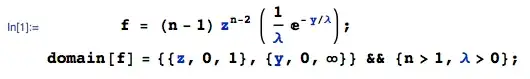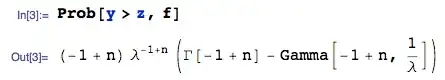2

Suppose $X_1,X_2,\ldots X_{n-1}\sim U(0,1)$, $X_n\sim \exp(\frac{1}{2})$. Else, suppose $X_1,X_2\ldots, X_n$ are independent. How can I calculate $P(X_n=\max(X_1,X_2\ldots, X_n))$

David
  • 82,662
user2135285
  • 21
  • Hint: http://math.stackexchange.com/questions/313390/probability-density-of-the-maximum-of-samples-from-a-uniform-distribution –  May 27 '14 at 06:16
  • 1
    Since X1...Xn-1 are independent samples of the same underlying distribution, you can use order statistics to get the distribution of the maximum among these n-1 numbers. The following page gives you the exact formula, along with a nice explanation. Once you get the distribution for the maximum number, then you can compare that to the distribution for Xn. But recognize that both distributions are continuous -- did you mean to write "less than or equal to" or "greater than equal to" instead? – user635185 May 27 '14 at 06:17

2 Answers2

3

The question's notation seems to encourage unnecessary confusion. It appears the OP is simply asking: what is the probability that the Exponential drawing is the sample maximum?

Let $(X_1, \dots, X_{n-1})$ denote a random sample of size $(n-1)$ drawn on a Uniform(o,1) parent, and let $Z = max(X_1, \dots, X_{n-1})$. It is well-known that the pdf of the sample maximum of size $n-1$ is: $(n-1) z^{n-2}$ defined on (0,1). Then, if $Y \sim Exponential(\lambda)$ and independent, then the joint pdf of $(Z,Y)$, say $f(z,y)$, is:

The problem

The probability that $Y$ is the sample maximum is: $P(Y>Z)$, which can be automatically computed as:

where Gamma[a,b] denotes the incomplete Gamma function.

Notes

  1. The Prob function used above is from the mathStatica package for Mathematica. As disclosure, I should add that I am one of the authors.

  2. There are 2 common (but different) parameterisations of the Exponential distribution, and the OP does not specify which is being used, so to avoid any confusion, I have solved for general parameter $\lambda$.

Glorfindel
  • 3,955
wolfies
  • 5,174
  • have you drawn the figures on your own, or are they taken from some source? If so, which utility did you use? Thanks! – nullgeppetto May 27 '14 at 07:57
  • @nullgeppetto The figures are also plotted using mathStatica/Mathematica, using the actual functional forms of the densities. – wolfies May 27 '14 at 08:03
1

Let $X=X_n$ and $Y=\max\{X_k\mid1\leqslant k\leqslant n-1\}$, then $(X,Y)$ is independent and $P(X\geqslant x)=\mathrm e^{-x/2}$ for every nonnegative $x$ hence $$ P(X\gt Y)=E(\mathrm e^{-Y/2}). $$ Furthermore $[Y\lt y]=\bigcap\limits_{k=1}^{n-1}[X_k\lt y]$ hence $P(Y\lt y)=y^{n-1}$ for every $y$ in $(0,1)$. Differentiating this yields the density of $Y$ and finally, $$ P(X\geqslant Y)=\int_0^1\mathrm e^{-y/2}\,(n-1)y^{n-2}\,\mathrm dy=2^{n-1}(n-1)\gamma(n-1,1/2), $$ where $\gamma(\ ,\ )$ is the (lower) incomplete gamma function.

Did
  • 279,727