3

In the inversive plane points $P$ and $P'$ are defined to be inverses with respect to a circle $\omega$ of radius $k$ and center $O$ when they are distinct from $O$, on the same ray emanating from $O$, and $OP * OP' = k^2$. When $\omega$ is a straight line (or circle of infinite radius), the operation of inversion is the same as a reflection (across the line). However, since the equation $OP * OP' = k^2$ breaks down with $O$ becoming the point at infinity when $\omega$ is a straight line, I am having trouble seeing the precise argument that is made to justify the equivalence of inversion and reflection in this case. Can anyone supply this argument?

3 Answers3

1

This is explained -- rather tersely -- in L. Ahlfors, Complex Analysis, McGraw-Hill, 3rd edition, 1979, pages 80-82. Identify the plane with the complex numbers. There is a theory of symmetries of the complex plane in which circles and lines have equal standing, namely the theory of fractional linear transformations. If $C_1$ is a line or circle and $C_2$ is another line or circle, then there is a fractional linear transformation taking $C_1$ to $C_2$; in fact there are many such transformations.

Theorem: Let $L$ be a line, let $C$ be a circle and let $T$ be a fractional linear transformation taking $L$ to $C$. Let $z$ and $z^*$ be a pair of points. Then $z$ and $z^*$ are related by reflection in the line $L$ if and only if $Tz$ and $Tz^*$ are related by inversion in the circle $C$.

Corollary: Let $C_1$ and $C_2$ be circles and let $T$ be a fractional linear transformation taking $C_1$ to $C_2$. Let $z$ and $z^*$ be a pair of points. Then $z$ and $z^*$ are related by inversion in $C_1$ if and only if $Tz$ and $Tz^*$ are related by inversion in $C_2$.

Corollary: Let $C$ be a circle and let $T$ be a fractional linear transformation taking $C$ to the real line. Then the transformation $$z \mapsto T^{-1}(\overline{Tz})$$ is inversion in $C$.

fred goodman
  • 4,253
1

This is a tricky problem, where the real question is, "Why should we define it as ..." rather than "Prove it is...." We can give motivation for the definition.

The first justification is continuity.

Let $P$ be a point on the line, and let $v$ be a a unit vector perpendicular to the line. For any radius, $r$, let $O_r$ be the point $P+rv$. Then the inversion of the circle with center $O_r$ and radius $r$ is a function on the plane. As $r\to\infty$, that function has, as a point-wise limit, the reflection through the line.

There isn't a single "point at infinity" in this case, but different points depending on the line's slope (specifically, different points at infinity, one per unit vector $v$.) That indicates that what we are looking at is something related to the projective plane, but I'm failing to recall a projective view of the inversion operation...

Thomas Andrews
  • 177,126
  • Not sure I follow: Since the line is the circle of inversion (with infinite radius), the infinite quantity is always present in $OP * OP' = k^2$, regardless of the radius of the circle with center $O_r$ ... ? –  May 26 '14 at 19:07
  • Again, I'm not talking about the line at all, but inversion of circles tangent to the line, as the radius approaches infinity. $k=r$ in this case. There isn't any useful $k$ when dealing with the line, because it has no radius. – Thomas Andrews May 26 '14 at 19:11
  • To give an idea of the way I was thinking about it, a "proof" might be based on identicality of the two half-planes determined by a line: A circle has an inside and an outside, but the two sides of a line are indistinguishable. Since inverting again with respect to the same circle gives the original point back, but the inside and outside of a circle are distinguishable, the distance from the point to the circle does not have to be the same distance as from the inverse point. However for a line, it would. Only a reflection can do this. This is not a proof ... –  May 26 '14 at 23:10
0

After researching this a bit I found a couple of explanations, one of which makes the most sense to me. However, one thing that is clear as Thomas Andrews points out in his answer, is that it is ultimately a definition, not a theorem. However in some ways it makes most sense to have this definition be the definition of inversion itself. If inversion is (equivalently) defined as below, then the equality of inversion and reflection does become a theorem (I believe).

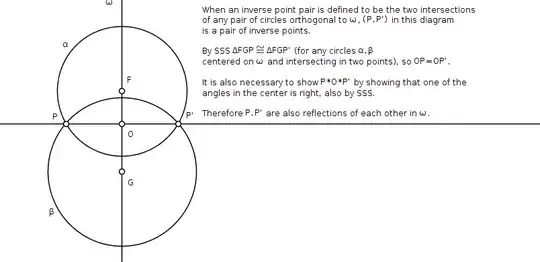
Explanation 1: It is possible to define inversion completely in terms of orthogonality: "Any point on $\omega$ is its own inverse, the inverse of any other point P is the second intersection of any two circles through P orthogonal to $\omega$. Replacing $\omega$ by a line, we deduce that reflection in a line may properly be regarded as a special case of inversion in a circle." (from Coxeter and Greitzer, Geometry Revisited). The easiest way for me to understand this explanation is to use this diagram.

enter image description here

Another explanation (from Pedoe, "A Course of Geometry") uses the concept of Harmonic Conjugates. The basic idea is if $A$ and $A'$ are diametrically opposite points on $\omega$ (with $\omega$ a circle, not a line), any pair of inverse points $(P, P')$ are harmonic conjugates with respect to $A$ and $A'$. As the radius of $\omega$ goes to $\infty$, $A'$ moves to $\infty$ along with O and $(P, P')$ become image points. I must admit that I don't understand this explanation for the same reason that I had trouble with my original conundrum: You wind up with saying something like $\frac{\infty}{\infty} = 1$ (or equally absurd).