0

Say we have some function $f:X\rightarrow Y$ where $C$ is a subset of $Y$. Can we always state that $f(f^{-1}(C))=C$?

johnnymath
  • 877
  • 3
    In http://math.stackexchange.com/questions/78110/ you ask almost the same thing. The same example could have been used in this answer (as Zev shows). – Asaf Karagila Nov 11 '11 at 05:18

2 Answers2

3

No, we can't - let $X=\{a\}$ and let $Y=\{b,c\}$, and let $f:X\to Y$ be defined by $f(a)=b$. Then $$f(f^{-1}(\{c\}))=f(\varnothing)=\varnothing\neq\{c\}\quad\text{and}\quad f(f^{-1}(Y))=f(\{a\})=\{b\}\neq Y$$ In general, we can only say that $f(f^{-1}(C))\subseteq C$. The statement $f(f^{-1}(C))=C$ holds for all subsets $C\subseteq Y$ if and only if $f$ is surjective.

For an arbitrary function $f$, these are the relations that hold. If you assume $f$ is injective, surjective, or both (i.e. bijective), some of the $\subseteq$'s and $\supseteq$'s turn into $=$'s.

Zev Chonoles
  • 129,973
0

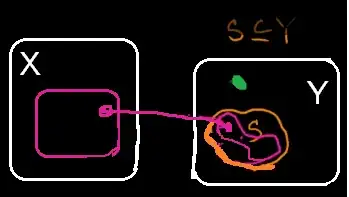
I thought to supplement the other answer with a picture.

The pink bespeaks both $f^{-1}(Y)$ and $f(a) = b$. Your $C$ is my $S$ in orange. The green point is $c \in Y$.

enter image description here