4

This is a follow-up to this question of mine: Cardinality of a minimal generating set is the cardinality of a basis

I observed in a comment to that question that it was, in fact, a duplicate of this question: Given a commutative ring $R$ and an epimorphism $R^m \to R^n$ is then $m \geq n$? (1)

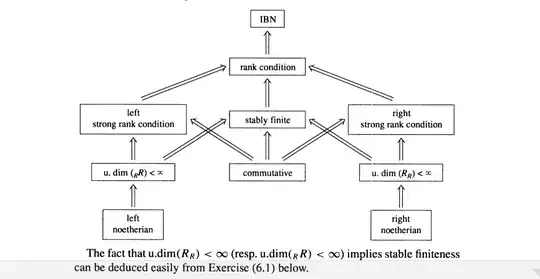
The proof uses heavily that the ring is commutative.

I am wondering now of an example of a ring with IBN where the answer to (1) is negative.

Motivation:

Arturo's answer to my previous question provides a reference to an article of Cohn (which I could only get a quarter of). However, he proves that there is no noetherian, artinian, or commutative (which we have already seen by different means) where (1) is negative.

The example of a ring which does not satisfy (1) that he gives does not have IBN.

But the cases in which he proves it affirmative are all classes of rings that have IBN! Can it be, then, that the answer to (1) is positive for every ring with IBN, or is there a ring with IBN where the answer to (1) is negative? (It would have to be a non noetherian, non artinian, noncommutative ring!)

Community
  • 1
Bruno Stonek
  • 12,527
  • Not-so-secret secret weapon: Lam, Lectures on modules and rings. I haven't looked where exactly he gives an example to show that the implication you ask about, can't be reversed, but I'm sure he does. – t.b. Nov 09 '11 at 23:00
  • 1
    @t.b. There it is, in page 11! Great. As expected, the example is quite nasty :) Thank you once again, Theo. You can perfectly post is as an answer, I'll accept it if in a safe time from now no one offers another (perhaps simpler?) example. – Bruno Stonek Nov 09 '11 at 23:40
  • @Bruno: The example in Theo's answer is very similar to a Leavitt algebra, about which you might have learned about in Córdoba recently :) – Mariano Suárez-Álvarez Nov 10 '11 at 04:54
  • @Mariano: Of course, Leavitt algebras appear in Cohn's paper, too, under the name $V_{1,n}$ --- Cohn refers to three papers of Leavitt's. – t.b. Nov 10 '11 at 14:26
  • @Mariano: Oh, I may have heard about them in Córdoba, in any case ;) A lot of things flew over my head there, unfortunately! – Bruno Stonek Nov 10 '11 at 23:31

1 Answers1

8

On Bruno's request I'm making my comment into an answer.

Invariant basis number and many related properties are studied in section 1.§1 of Lam's Lectures on modules and rings, they are summarized in this diagram on page 17 in which none of the implications can be reversed:

Implications between IBN and other properties

The example showing that invariant basis number does not imply the rank condition is as follows (it appears on page 11 after proposition 1.24:

Let $R$ be the $\mathbb{Q}$-algebra with generators $a,b,c,d$ and relations $$ ac=1, \quad bd=1, \quad ad = 0 = bc $$ so that we have $$ \begin{bmatrix} a \\ d \end{bmatrix} \begin{bmatrix} c & d \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}. $$ This shows that $\begin{bmatrix} a \\ d\end{bmatrix}: R \to R^2$ is an epimorphism so that the rank condition fails.

The proof that $R$ does have invariant basis number is given in P.M. Cohn, Some remarks on the invariant basis property, Topology 5 (1966), 215–228, MR197511.

Cohn denotes this ring by $U_{1,2}$ in §5. The proof that it has invariant basis number involves deriving a normal form for elements of $R$ and showing that the trace of $1 \in R$ (i.e., the image of $1$ in the abelian group $R/[R,R]$) has infinite order. It is a bit too laborious for me to reproduce it here. The argument is given before Lemma 5.1. By the Corollary in §3 (or Lam's Exercise 5 on page 17) this implies that $R$ has invariant basis number.

See also the comments to this related MO thread.

Community
  • 1
t.b.
  • 78,116