$n$th prime bounded from above?

Asked May 21 '14 at 15:05

Active May 21 '14 at 22:13

Viewed 81 times

Let $p_n$ be the $n$th prime, $p_n\#\equiv\prod_{k=1}^{n}p_k$ (primorial), and $\sigma(n)=\sum_{d|n}^{}d$ (divisor function).

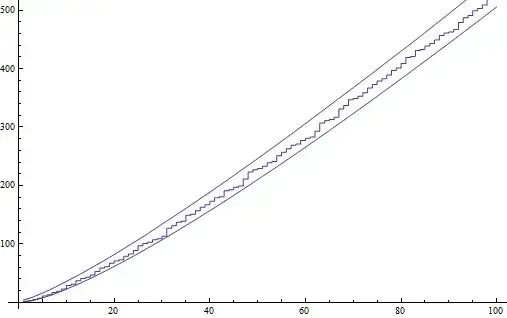
Does $\text{exp}\bigg(\dfrac{\pi^2}{6 e^{\gamma}}\dfrac{\sigma(p_n\#)}{p_n\#}\bigg)$ bound $p_n$ from above?

(Note: From Daniel Fischer's answer here.)

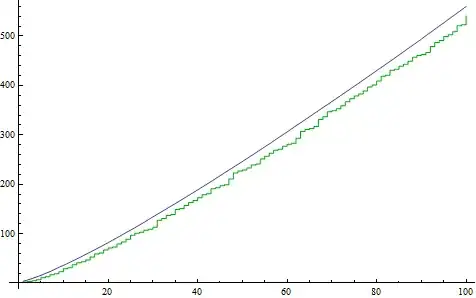
enter image description here

Update

... and from below by $\log(p_n\#)$?

enter image description here

edited Jun 12 '20 at 10:38

Community

asked May 21 '14 at 15:05

martin

Is the constant $\frac{\pi^2}{6e^{\gamma}}$ experimental? (just asking). Also, is $\gamma$ supposed to be the Euler-Mascheroni constant? – chubakueno May 21 '14 at 15:09
No - it is from Daniel Fischer's answer here. And yes to the second :) – martin May 21 '14 at 15:11
Since $\sigma$ is multiplicative, $\sigma(p_n#)/p_n#$ is just an obscure way of writing $$\prod_{i=1}^n \left(1 + \frac{1}{p_i} \right) $$ – May 21 '14 at 22:20