If the expansion of the logarithmic integral is$$\text{li}(n) = \log \log n + \gamma + \sum_{k=1}^\infty \dfrac{(\log n)^k}{k! k}$$ what is the inverse of the function?
-
1See http://math.stackexchange.com/questions/94860/inverse-function-of-operatornamelix-over-x-mu, there is AFAIK no closed form. – gammatester May 21 '14 at 14:16
-
Great - thanks. – martin May 21 '14 at 14:42
3 Answers
$$\operatorname{Li}^{-1}(x)= x\biggl[\ln(x)+\ln_{2}(x)-1+\sum_{j=1}^{m}\frac{(-)^{j-1}P_{j}(\ln_{2}(x))}{\ln(x)^{j}}+o\biggl(\frac{1}{\ln(x)^{m}}\biggl)\biggl]$$ $$\operatorname{Li}^{-1}(x)\sim x\biggl(\ln(x)+\ln_{2}(x)-1+\frac{\ln_{2}(x)-2}{\ln(x)}-\frac{\ln_{2}(x)^{2}-6\ln_{2}(x)+11}{2\ln(x)^{2}}+ \ldots\biggl)$$
where $\ln_{2}(x)=\ln (\ln(x))$
http://mathworld.wolfram.com/PrimeFormulas.html go to (15) paragraph https://www.emis.de/journals/JIPAM/images/153_02_JIPAM/153_02.pdf
- 31,845
- 1,579
-
2thanks - yes, should have self-answered really! Thanks for adding for sake of completion. +1 of course :) – martin Sep 13 '17 at 09:43
For $y(\text{li}(c))=c$, we may get a different branch if $c<0,0\le c<1,c>1$ etc. $$\text{li}(y)=x\implies y’=\ln(y),y=\sum_{n=0}^\infty\frac{y^{(n)}(a)(x-a)^n}{n!}$$
then coefficients are:
$$y(a)=c\\y’(a)=\ln(y(a))=\ln(c)\\y’’(a)=\frac{y’(a)}{y(a)}=\frac{\ln(c)}{c}\\y’’’(a)=\frac{y’’(a)}{y(a)}-\frac{y'(a)^2}{y^2(a)}=\frac{\ln(c)}{c^2}-\frac{\ln^2(c)}{c^2}\\y^{(4)}(a)=\frac{y^{(3)}(a)}{y(a)}+\frac{2y’(a)^3}{y^3(a)}-\frac{3y’(a)y’’(a)}{y^2(a)}=\frac{2\ln^3(c)}{c^3}-\frac{4\ln^2(c)}{c^3}+\frac{\ln(c)}{c^3}\\\vdots\\y^{(n)}(a)=\frac1{c^{n-1}}\sum_{m=1}^{n-1}a_m\ln^m(c)$$
Therefore:
$$y=c+\ln(c)(x-a)+\frac{\ln(c)}{c}\frac{(x-a)^2}2+\left(\frac{\ln(c)}{c^2}-\frac{\ln^2(c)}{c^2}\right)\frac{(x-a)^3}9+\left(\frac{2\ln^3(c)}{c^3}-\frac{4\ln^2(c)}{c^3}+\frac{\ln(c)}{c^3}\right)\frac{(x-a)^3}{12}+\dots$$
Which works. The graph uses $4$ terms only:
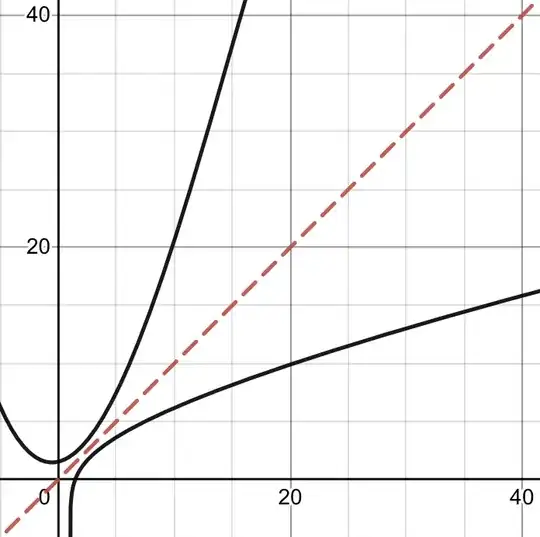
- 12,081
the inverse is $n(\ln(n)+\ln(\ln(n)-1)$ approximately, as $\pi(x)\sim \operatorname{li}(x)$ where $\pi(x)$ is prime counting function,thus the above formula is an approximate for the $n$th prime and hence asymptotical to inverse of $\operatorname{li}(x)$.
-
1(you meant $li(x) \approx \pi(x)$ so $ li^{-1}(n) \approx \pi^{-1}(n) = p_n$ where $p_n$ is the $n$-th prime) – reuns Aug 08 '17 at 13:05