The circle with radius 1 and center $(0,0,1)$ in the plane $x+y+z=1$ can be parametrized by
\begin{align}
\vec{p}(t) &= \langle 0,0,1 \rangle + \cos(t)\langle 1,-1,0 \rangle/\sqrt{2} + \sin(t) \langle 1,1,-2 \rangle/\sqrt{6} \\
&= \left\langle \frac{\sin (t)}{\sqrt{6}}+\frac{\cos
(t)}{\sqrt{2}},\frac{\sin (t)}{\sqrt{6}}-\frac{\cos
(t)}{\sqrt{2}},1-\sqrt{\frac{2}{3}} \sin (t) \right\rangle.
\end{align}
It's shadow can be parametrized by just dropping the $z$ coordinate.
$$\vec{s}(t) = \left\langle \frac{\sin (t)}{\sqrt{6}}+\frac{\cos
(t)}{\sqrt{2}},\frac{\sin (t)}{\sqrt{6}}-\frac{\cos
(t)}{\sqrt{2}} \right\rangle.$$
This is enough to visualize.
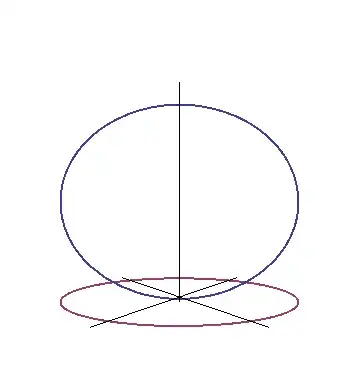
Once we have the parametrization, we can generate points on the ellipse by simply plugging in $t$ values. Here are five points on the ellipse in the plane, for example.
$$
\begin{array}{l|l}
t & (x,y) \\
\hline
0 & \left(\frac{1}{\sqrt{2}},-\frac{1}{\sqrt{2}}\right) \\
\hline
\frac{\pi }{3} & \left(\frac{1}{\sqrt{2}},0\right) \\
\hline
\frac{\pi }{2} & \left(\frac{1}{\sqrt{6}},\frac{1}{\sqrt{6}}\right) \
\\
\hline
\pi & \left(-\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}}\right) \\
\hline
\frac{3 \pi }{2} & \left(-\frac{1}{\sqrt{6}},-\frac{1}{\sqrt{6}}\right)
\end{array}
$$
Since five points determine an ellipse, we can find the Cartesian formula easily enough. My favorite technique is to set the following determinant equal to zero.
$$
\left|
\begin{array}{cccccc}
x^2 & x y & y^2 & x & y & 1 \\
\frac{1}{2} & -\frac{1}{2} & \frac{1}{2} &
\frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} & 1 \\
\frac{1}{2} & 0 & 0 & \frac{1}{\sqrt{2}} & 0 & 1 \\
\frac{1}{6} & \frac{1}{6} & \frac{1}{6} &
\frac{1}{\sqrt{6}} & \frac{1}{\sqrt{6}} & 1 \\
\frac{1}{2} & -\frac{1}{2} & \frac{1}{2} &
-\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} & 1 \\
\frac{1}{6} & \frac{1}{6} & \frac{1}{6} &
-\frac{1}{\sqrt{6}} & -\frac{1}{\sqrt{6}} & 1 \\
\end{array}
\right|
$$
After some simplification, this yields
$$
2 x^2 + 2 xy + 2 y^2 = 1.
$$
