Why is $\cos(x)$ the derivative of $\sin(x)$?

Question

The derivative of $\sin(x)$ is $\cos(x)$, and the derivative of $\cos(x)$ is $-\sin(x)$. Is there a simple proof of this, preferably using pictures?

Answer 1

The point $(\cos x,\sin x)$ moves around the circle as $x$ increases. If $x$ is in radians, then the rate at which it moves is $1$, since that's how radians are defined. The direction in which it moves is tangential to the circle, pointing counterclockwise. Supposing $a^2+b^2=1$, so $(a,b)$ is on the circle, and one is moving counterclockwise along the circle through that point. Then one's direction, tangential to the circle, is at right angles to the radius vector from $(0,0)$ to $(a,b)$. If you turn that vector $90^\circ$ counterclockwise, you get $(-b,a)$. Thus it is $(-\sin x,\cos x)$. The rate of change is thus $$ \frac{d}{dx}(\cos x,\sin x) = (-\sin x,\cos x). $$

If one uses some other units than radians, one moves faster or slower, but in the same direction. Thus instead of the unit vector $(-b,a)$, one gets a non-unit vector $c(-b,a)$, thus $c(-\sin x,\cos x)$. In other words, if something other than radians is used, we have $$ \frac{d}{dx}\cos x = -c\sin x $$ for some constant $c$.

Answer 2

$$f(x)=\cos x$$ Then $$f'(x)=\lim_{h\to 0}\frac{\cos(x+h)-\cos(x)}{h}=\lim_{h\to 0}\frac{-2\sin\frac{h}{2}\sin\frac{2x+h}{2}}{h}=-\sin x$$

Since, with no use of derivatives, one can prove that $$\lim_{t\to 0}\frac{\sin t}{t}=1$$

Answer 3

The picture you can use is the graphs of $\sin$ and $\cos$ juxtaposed. You should have been taught how to draw the derivative of a function from the graph of another one.

For instance, you know that at $\pi/2$ $\sin$ achieves a local max, and so the graph of the derivative should pass through $0$ there, as happens (see the picture below). This gives the shape, then use that $\cos(0)=1$.

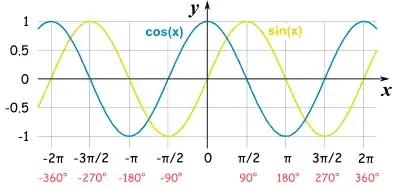
It should be noted thought that it all depends on the definitions of these functions which you've been given to work with. If it is the series definition then you could demonstrate the property by doing a term by term differentiation, after justifying that the derivative and sum commute.