3

We are given vector space of polynomials over $\mathbb R$ of two variables with powers not higher than 2013.
Let's consider subspace $V$ which contains such polynomials $f$, so following holds for them:
$$\oint_{C} f(x,y)ds =0$$ Where $C = \{x^2+y^2 = R^2\}$.
Task is to find dim $V$.

First I must note that I felt undereducated for that problem when I first approached it, so I went through some books and materials and came up with solution.
Solution
I moved to polar coords and with use of the following formula I was able to write the required equation
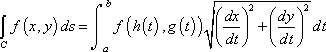
formula
$$R\int_0^{2\pi}\sum_{k_1=0; k_2=0}^{2013}{a_{k_1 k_2}R^{k_1k_2}cos^{k_1}t \cdot sin^{k_2} t\space dt} = 0$$ By the way, I have doubts that this formula applies there. But if it is, $$cos^{p}(0)=cos^p(0);\space sin^{p}(2\pi)=sin^p(2\pi)$$
Hence, it's a trivial subspace and any polynomial fits.
Than, power spans from $0$ to $2013$ for both variables and basis should have all of them, than $dim V = 2013^2$
I have doubts about it's correctness, but my main concern is understanding. So I would appreciate hints and corrections.

Dmitri K
  • 1,401
  • Where did you get it, seems interesting. And, what is $C$ here? Unit circle? – PA6OTA May 16 '14 at 16:19
  • @PA6OTA Sorry, I forgot $C$ definition. Yes, it's circle with radius R. Already made a fix in question. This task is from Yandex school of data analysis. – Dmitri K May 16 '14 at 16:23

3 Answers3

7

Sketch:

  • Let $X$ be the vector space of all polynomials with powers up to 2013. Verify that $X$ has dimension $2014^2$ (remember to count the 0 power).

  • Let $T : X \to \mathbb{R}$ be the map $Tf = \oint_C f$. Verify that $T$ is linear and surjective (i.e. its range is all of $\mathbb{R}$). (For surjectivity, it suffices to find a single $f$ such that $Tf \ne 0$).

  • Observe that $V$ is the kernel (null space) of $T$.

  • Recall the rank-nullity theorem.

Nate Eldredge
  • 97,710
  • That's brilliant. Would you take a look at what I've got: $rk(T) + null(T) = dim(X)$. $dim(X)$ as you said, is $2014^2$ and rank of mapping $T$ is what I have trouble with. I found myself thinking about that as hard as I can for more than an hour. But probably I'm not deep enough in the set theory now. So I would appreciate pointer about calculating $rk(T)$. While thinking, I thought of another way - find $dim(V)$ directly - it's all possible polynomials with constraint: "there could not be an element having even powers for x and y both". But your way is of more beauty) – Dmitri K May 16 '14 at 18:50
  • The rank is easier than you think. What's the definition of the rank of a linear transformation? As for your other characterization, I don't think it works: a polynomial of the form $x^2 y^2 +c$ will integrate to 0 for the right choice of the constant c. – Nate Eldredge May 16 '14 at 19:06
  • For linear transformation rank is amount of linearly independent rows/cols. But since $T$ is mapping polynomials to numbers, I honestly fail to see it as linear transform... Concerning that another way - yes, I agree with your objection. – Dmitri K May 16 '14 at 19:21
  • Hint: the real numbers are a vector space of dimension 1. – Nate Eldredge May 16 '14 at 20:11
  • $T: X \to \mathbb{R}$. $T(x) = Ax$ So we could consider element of X as column of coefficients $a_{ij}$, and A as row of according length. Then, it's clear that $rk(A)=1$. Also I find another definition of the rank of linear mapping: $rk(T)=dim(Im(T))$. Image of T would be $\mathbb{R}$, so according to your suggestion, this also gives $rk(T)=1$. Than $dim(V)=null(T)=2014^2-1$. But I still have doubts, though. We state that $dim(\mathbb{R})=1$. That holds when R is vector space over which field? I found proofs for space R over Q dim(R) is infinite. http://math.stackexchange.com/questions/6244 – Dmitri K May 17 '14 at 08:09
  • Also, It seems slightly counter-intuitive, that answer not depend on actual integral, so it looks to me that we would have the same answer for another $C$? Is that correct? Nate, thanks for your explanations and patience, by the way:) – Dmitri K May 17 '14 at 08:12
  • @wf34: you've got it! Yes, I'm assuming we're working over R; that's the most reasonable interpretation of this question. Over Q, yes, everything in sight would have infinite dimension. And yes, the answer would be the same for almost any other integral. – Nate Eldredge May 17 '14 at 15:36
0

Well, the dimension is certainly not $2013*2013$. For example, even-powered polynomials $x^{2n} y^{2m}$ certainly do not integrate to 0.

Hint: what do you know about $\int_0^{2\pi} \sin^p\!\theta \cos^q\!\theta \, d\theta$?

Hint2: apply integration by parts twice to reduce $\int_0^{2\pi} \sin^p\!\theta \cos^q\!\theta \, d\theta$ to $\int_0^{2\pi} \sin^{p-2}\!\theta \cos^{q+2}\!\theta \, d\theta$

PA6OTA
  • 1,972
  • 10
  • 12
0

The given integral equation imposes a single linear condition. You just need to check that the relation is not trivial by finding a polynomial whose integral is nonzero.

Rene Schipperus
  • 39,526