Rational approximation of $\tanh\,(\sqrt[4]{s}$)

Question

I'd like to find a rational representation of

$$f(s) = \frac{\tanh\,\sqrt[4]{s}}{\sqrt[4]{s}}= \frac{a_0 + a_1 s + a_2 s^2 + ... + a_n s^n}{b_0 + b_1 s + b_2 s^2 + ... + b_m s^m} $$

For the case $$f(s) = \tanh\,\sqrt{s}$$ I solved the problem with this answer - the Padé approximation seems perfect, as all $z$ in the resulting function have the power 2 or 0 - so I can get rid of the square root. $$\tanh\,z\approx\mathcal{T}_3(z)=\frac{z(600 + 70 z^2 + z^4)}{600+270z^2+11z^4+\frac{z^6}{24}}$$ $$\frac{tanh\,\sqrt{s}}{\sqrt{s}} \approx \frac{600 + 70 s + s^2}{600 + 270 s + 11 s^2 + \frac{1}{24} s^3} $$

But I'm really struggling for the case $\frac{\tanh\,\sqrt[4]{s}}{\sqrt[4]{s}}$.

For discrete values Matlab offers a nice fit via Least-Squares:

  f(x) =  (p1*x^5 + p2*x^4 + p3*x^3 + p4*x^2 + p5*x + p6) /
          (x^5 + q1*x^4 + q2*x^3 + q3*x^2 + q4*x + q5)

Coefficients (with 95% confidence bounds):
       p1 =      0.1091  (0.1087, 0.1095)
       p2 =       155.8  (22.49, 289.2)
       p3 =        4829  (-1.874e+05, 1.971e+05)
       p4 =      -493.8  (-5.957e+06, 5.956e+06)
       p5 =        1442  (-1.922e+06, 1.925e+06)
       p6 =      -441.9  (-8.783e+06, 8.782e+06)
       q1 =       521.7  (-705.4, 1749)
       q2 =        6467  (-6.379e+05, 6.508e+05)
       q3 =       309.6  (-7.915e+06, 7.916e+06)
       q4 =      -735.6  (-1.378e+06, 1.376e+06)
       q5 =       636.3  (-9.718e+06, 9.72e+06)

Goodness of fit:
  SSE: 0.006849
  R-square: 0.9993
  Adjusted R-square: 0.9993

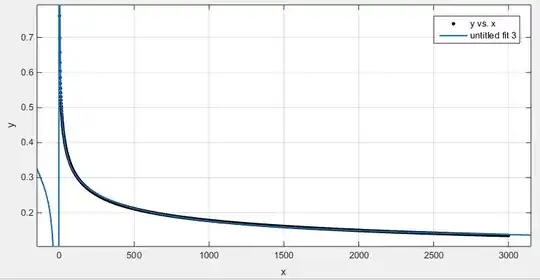
enter image description here

But isn't it possible to achieve the same analytical?

My range of s is 50 to at least 3000.

I'd appreciate any hints! Thank you!

For the continued fraction case 2 simply substitute and get $$\frac{\tanh\sqrt{z}}{\sqrt{z}}=\cfrac{1}{1+\cfrac{z}{3+\cfrac{z}{5+\cdots}}}$$ — gammatester, May 15 '14 at 10:52
@gammatester: have a look at my edit, that won't solve my problem. — Robert Seifert, May 15 '14 at 11:17

score 1 · Answer 1 · answered May 15 '14 at 16:35

1

The Maple code $$Digits := 20: with(numapprox):$$ $$CP := minimax(tanh(s^{1/4)}/s^{1/4}, s = 50 .. 3000, [3, 3]): B := convert(normal(CP), rational); $$ produces $$ {\left( {\frac {23656183}{36522077940}}+{\frac {18006439\,s}{ 1317511518722}}+{\frac {884573\,{s}^{2}}{33615169193146}}+{\frac {9149 \,{s}^{3}}{2475624657857145}} \right) / \left( {\frac {78515143}{ 72675755899}}+{\frac {74718691\,s}{1641283916311}}+{\frac {1988992\,{s }^{2}}{12741186399775}}+{\frac {31619\,{s}^{3}}{679467812897445}} \right) } $$ and $$Optimization:-Maximize(abs(tanh(s^{1/4})/s^{1/4}-B), s = 50 .. 3000) $$ gives $$[ 0.00001941974017751662,[s= 1235.5439648649823922]].$$

answered May 15 '14 at 16:35

user64494

5,811

It's also a numerical solution. Possible, but should be the last option. This approximation is part of a bigger problem of my thesis, but as a analytical solution is desired I hope to find something similar to the case above. Thanks anyway! – Robert Seifert May 15 '14 at 17:11
In many cases so-called analytical solutions are of sacred cows which produce a bit of milk. – user64494 May 15 '14 at 17:18
usually I think the same ;) but when it comes to the final thesis... and it seems solvable. – Robert Seifert May 15 '14 at 17:49
Take a look at the Remez algorithm used by the minimax command of Maple. – user64494 May 15 '14 at 18:20

Rational approximation of $\tanh\,(\sqrt[4]{s}$)

1 Answers1