8

In the course of doing some calculations comparing unrepeatable sets of event trials, I ended up with the following identity. If my reasoning and my math are correct then this ought to be true, and it is indeed true for several values of $k$ and $l$ that I tried in it. But I don't know how to prove it.

$${k + l + 1 \choose l} \sum_{m = 0}^l \frac{ {k + m \choose k}} {{l + 2k + 2 + m \choose {2k + 2}}} = 1.$$

I am familiar with the identity

$$\sum_{m = 0}^l {k + m \choose k} = {k + l + 1 \choose l}$$

and even as I'm writing this I'm considering ways of using it in a proof of this identity, but my prospects don't look good for getting there. Seeing how a proof of this is done may serve as the basis of dramatically simplifying my results. How to prove this?

user150200
  • 111

1 Answers1

3

First, express the sum throuh hypergeometric functions. \begin{align} & \sum_{m = 0}^l \frac{ {k + m \choose k}} {{l + 2k + 2 + m \choose {2k + 2}}} = \frac{(2k+2)!}{k!}\sum_{m = 0}^l\frac{(k+m)!(l+m)!}{m!(l+2k+2+m)!}=\\ &\frac{(2k+2)!}{k!} \left(\sum_{m = 0}^\infty \frac{(k+m)!(l+m)!}{m!(l+2k+2+m)!}-\sum_{m = l+1}^\infty\frac{(k+m)!(l+m)!}{m!(l+2k+2+m)!}\right). \end{align} Using Pochhammer symbol $(x)_n=x(x+1) ... (x+n-1)$ one obtains $$ \sum_{m = 0}^\infty \frac{(k+m)!(l+m)!}{m!(l+2k+2+m)!}=\frac{k!l!}{(l+2k+2)!}\sum_{m = 0}^\infty \frac{(k+1)_m(l+1)_m}{m!(l+2k+3)_m}=\\ \frac{k!l!}{(l+2k+2)!} \phantom{}_2F_1\left({\textstyle k+1,l+1 \atop \textstyle l+2k+3}\,;1\right), $$ $$ \sum_{m = l+1}^\infty\frac{(k+m)!(l+m)!}{m!(l+2k+2+m)!}=\frac{(k+l+1)!(2l+1)!}{(l+1)!(2l+2k+3)!}\sum_{m = 0}^\infty\frac{(k+l+2)_m(2l+2)_m}{(l+2)_m(2l+2k+4)_m}=\\ \frac{(k+l+1)!(2l+1)!}{(l+1)!(2l+2k+3)!} \phantom{}_3F_2\left({\textstyle k+l+2,2l+2,1 \atop \textstyle l+2,2l+2k+4}\,;1\right). $$ Due to Gauss' theorem $$ \phantom{}_2F_1\left({\textstyle k+1,l+1 \atop \textstyle l+2k+3}\,;1\right)=\frac{(l+2k+2)!k!}{(2k+1)!(l+k+1)!}. $$ The second series can be summed using Watson's theorem 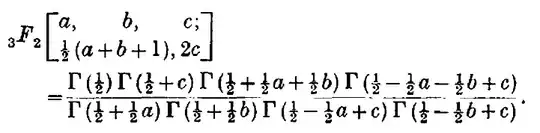enter image description here

by substituting $c=k+l+2,\ a=1, \ b=2l+2$ and simplifications: $$ \phantom{}_3F_2\left({\textstyle k+l+2,2l+2,1 \atop \textstyle l+2,2l+2k+4}\,;1\right)=\frac{(l+1)!k!(2k+2l+4)!(l+1)!(k+1)!}{(k+l+1)!(k+l+2)!(2l+2)!(2k+2)!}. $$ Finally substituting these values for hypergeometric functions and simplifications one obtains $$ \sum_{m = 0}^l \frac{ {k + m \choose k}} {{l + 2k + 2 + m \choose {2k + 2}}}=\frac{2}{{k + l + 1 \choose l}}-\frac{1}{{k + l + 1 \choose l}}=\frac{1}{{k + l + 1 \choose l}}. $$

Martin Nicholson
  • 3,883