6

Say we have a metal bar in space aligned horizontally and we start rotating it counter-clockwise about its left end. Then, the sin of the angle from between the horizontal and the bar is the y coordinate of the far end divided by the length of the bar. So, I understand that sin/cos are related to projections of things when you rotate them. Is this the fundamental idea? Why do sin curves look the way they do? Why is the slope most negative when sin(x) = 0? I'm looking for an intuitive answer, not just that the derivative of sin is cos.

RustyDoorknobs
  • 193
  • 1
    The $y$-coordinate is changing most rapidly when the moving end of the bar is on the $x$-axis, when the bar is horizontal. This is reasonably clear from visualization, and does not require taking the derivative. Similarly, it is visually clear that the rate of change is $0$ when the bar is vertical. – André Nicolas May 15 '14 at 01:44
  • When dealing with the trigonometric functions you must always go back to their definitions in terms of right triangles. The shape of the sinusoid is determined by that definition and I don't think you can really make sense of the shape other than that they are equivalent. – Jared May 15 '14 at 01:47
  • 3
    @Jared: ... or their definitions in terms of circles. –  May 15 '14 at 02:07
  • @Hurkyl The unit circle is helpful when thinking of trigonometric functions but we make sense of the unit circle through the elementary definitions from right triangles. – Jared May 15 '14 at 02:13
  • 1
    Now one caveat to what I said is that it's hard to make sense of trigonometric functions at all when we start talking about complex values. At that point we sort of have to trust the algebra. I don't think there's anyway to argue, fundamentally (from right triangles), that $\sin(x) = \frac{e^{ix} - e^{-ix}}{2i}$...for that we have to trust the algebra of Euler's equations. – Jared May 15 '14 at 02:17
  • Answer: because that is how the sin curve was defined. It’s a function from real numbers to the subset of real numbers between -1 and 1. Right there that constrains a lot of the properties of the function and it’s graph. – marshal craft Apr 10 '22 at 10:32

3 Answers3

41

Yes, that's the idea. The end of the bar is moving at a constant speed, so the $y$ component of its velocity (which is the rate of change of $\sin(\theta)$) is greatest in magnitude when all of that velocity is in the $y$ direction, and that happens when $\sin(\theta) = 0$.

enter image description here

Robert Israel
  • 448,999
8

Graphically you can see that at $\theta = 0$ the derivative of the $\sin$ (the $y$-value) is changing the most as opposed to anywhere else (other than the other side of the circle at $\theta = \pi$):

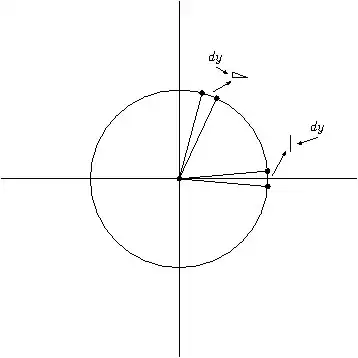
Graph of unit circle with derivative

Here's another picture which shows that the shape of the sinusoid is due to the definition of sine in the first quadrant (forgive the approximate nature of this sketch--but it is basically correct):

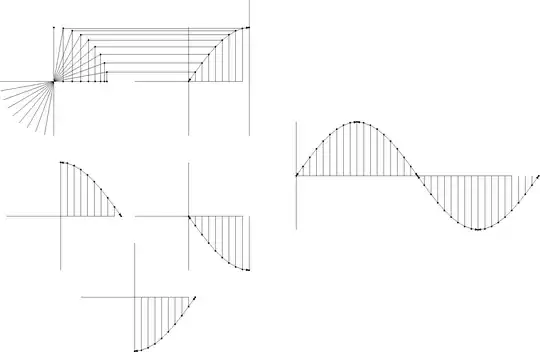
enter image description here

Jared
  • 6,227
3

I think the other answers fully answer the question, but this might be helpful. My favorite real-life visualization of a sin curve comes from a telephone handset cable:

enter image description here

When stretched out on a flat surface, and viewed from above, the shape of the cable approximates a sin curve. The equations for the center of the cable will be something like:

$$y=R\sin(Ax)$$ $$z=R\cos(Ax)$$

where R is the radius of the cable spiral, and A depends on how much the cable is stretched.

Ilmari Karonen
  • 26,117
Digital Trauma
  • 193
  • 9
    Soon enough you'll need to explain what a telephone handset cable is... – Joe May 15 '14 at 17:33
  • 1
    @Joe it's the waves representing modulated signal transmitted from my smartphone, right? – OJFord May 15 '14 at 17:36
  • @Joe perhaps I should add an image like this to clarify http://upload.wikimedia.org/wikipedia/commons/8/8a/1979_TMA7214_706_Style_Two_Tone_Grey_Rotary_Dial_Telephone.JPG ;-) – Digital Trauma May 15 '14 at 17:46
  • 2
    @Joe I can see it now. I can't wait to say to my kids: "Phones weren't always wireless y'know! Back in my day phone service came directly to the house through physical cables! And you could only walk a few feet from the phone, because it was connected to the wall!" – Cruncher May 15 '14 at 20:30
  • Fun Fact: Contemplating a telephone handset cable —specifically, the idea that rotating the helix along its axis induces a phase shift in the projected curve— is what initially inspired this visualization of the derivatives of sine and cosine. – Blue Apr 10 '22 at 10:30