2

I'm trying to understand this answer which I copy here (I didn't ask to the user because he left MSE).

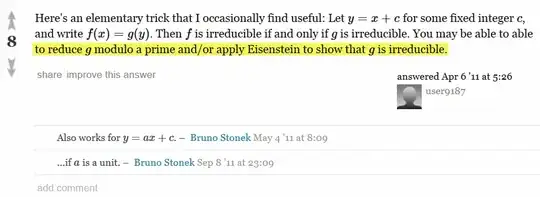
Could someone verify if my answer is correct and help me to understand the highlighted statement, maybe giving me a concrete example?

My attempt:

$\Leftarrow$

If $f$ is reducible, then $f(x)=h_1(x)h_2(x)=g(x+c)$, then $g(x)=h_1(x-c)h_2(x-c)$, so $g(x)$ is reducible.

$\Rightarrow$

If $g(x)$ is reducible, then $g(x)=h_1(x)h_2(x)=f(x-c)$, then $f(x)=h_1(x+c)h_2(x+c)$, so $f(x)$ is reducible.

Thanks in advance

Community
  • 1
user75086
  • 823
  • Your understanding is correct. As an example, consider the polynomial $$X^4+6X^3+14X^2+20X+21.$$ It is irreducible, which is easier to see after translating over $-1$. – Servaes May 14 '14 at 18:37
  • Your proof is correct and "translating" the polynomial opens up applying criteria like Eisenstein's or reducing mod a prime. – Nicky Hekster May 14 '14 at 18:37
  • @Servaes As an example I meant by this statement: "reduce g modulo a prime and/or apply Eisenstein to show that g is irreducible", can you give me an example what he means? thank you – user75086 May 14 '14 at 21:03
  • @NickyHekster What do you mean by " reducing mod a prime"? – user75086 May 14 '14 at 21:12

1 Answers1

1

Yes, that's the idea. Basically we are exploiting the fact that the shift map, being an automorphism, faithfully preserves multiplicative structure. Note that you also have to argue that the images of the factors remain nonzero nonunits for the proof to be complete.

Bill Dubuque
  • 272,048
  • I didn't understand what the uses means by "reduce g modulo a prime and/or apply Eisenstein to show that g is irreducible", can you give me an example what he means? thank you – user75086 May 14 '14 at 21:00
  • @user75086 Similar to your proof, if $,f,$ is reducible then it will remain reducible mod $p$ as long as the degrees don't drop, i.e. $,p,$ doesn't divide the leading coefficient. Then, contrapositively, irreducible mod $p$ $,\Rightarrow,$ irreducible. Ditto for any multiplicative map that doesn't map a nonunit to a unit. – Bill Dubuque May 14 '14 at 21:29
  • That's the main trouble in my question, what it means a polynomial be irreducible mod $p$? – user75086 May 14 '14 at 21:34
  • @user75086 It means that it is an irreducible element when mapped into $,\Bbb F_p[x],,$ i.e. a nonunit $\ne 0$ with only trivial factorizations, i.e. $,f = gh,\Rightarrow, g\mid 1,$ or $,h\mid 1,,$ or, equivalently, $,f\mid h,$ or $,f\mid g,,$ i.e. the only factors of $,f,$ are units or associates of $,f.\ \ $ – Bill Dubuque May 14 '14 at 21:39
  • I hope not asking too much, but can you give a concrete example of what you have just said? – user75086 May 14 '14 at 22:45
  • @user75086 $\ {\rm mod}\ 3!:\ f(x) = x^3-x+1, $ is the constant function $1,$ so has no roots mod $3,,$ so is irreducible mod $3,,$ so is irreducible over $,\Bbb Q.\ \ $ – Bill Dubuque May 14 '14 at 23:14
  • Do you know some books which I can find more this stuff? – user75086 May 14 '14 at 23:57
  • @user75086 Quotient (residue) rings are discussed in every abstract algebra textbook. These facts about irreducibility often occur as exercises. – Bill Dubuque May 15 '14 at 01:05