4

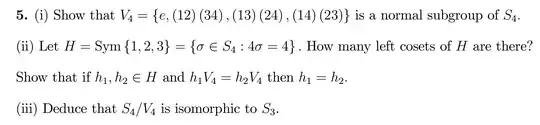
enter image description here

I have managed to do part i and ii. In part ii, the number of left cosets of H is 4.

I am stuck with part iii. I am guessing I will have to use first isomorphism theorem but not sure how.

$V_4$ is the potential kernel as it is normal subgroup (part i) But now i am not sure on what to do next. Do I have to find homomorphism from $S_4$ to some group such that that group has a subgroup $S_3$? But then how do I show that this is actually isomorphic to S4/V4 ?

Thanks. I am confused about first isomorphism theorem.

user147016
  • 41
  • 1
    Andreas Caranti's answer is the way to do this the way part (ii) leads to part (iii). For different approached to (iii) see the questions listed as related on the sidebar. This seems to be missing, so I add it this way. The same arguments have probably been written many times over in this site. This is a common exercise and comes with different sets of hints - all emphasizing slightly different aspects. – Jyrki Lahtonen May 14 '14 at 11:15

2 Answers2

6

Suppose $$ h_{1} V_{4} = h_{2} V_{4} ,$$ with $h_{1}, h_{2} \in H$. Then $h_{2} = h_{1} v$ for some $v \in V_{4}$. Therefore $$ 4 = 4 h_{2} = 4 h_{1} v = 4 v. $$ But the only element $v \in V_{4}$ that fixes $4$ is $v = e$, so $h_{2} = h_{1} e = h_{1}$.

Now you know that there are $6$ distinct cosets $h V_{4}$, for $h \in H$. Since $\lvert S_{4} : V_{4} \rvert = 6$, all cosets of $V_{4}$ are of this form, and thus $S_{4} = V_{4} H$. It follows (or you can check) that $V_{4} \cap H = \{ e \}$. Therefore $$ \frac{S_{4}}{V_{4}} = \frac{V_{4} H}{V_{4}} \cong \frac{H}{V_{4} \cap H} = \frac{H}{\{ e \}} \cong H. $$ Here I have used the second isomorphism theorem.

Andreas Caranti
  • 68,873
4

As an alternative way to show $(iii)$;

$S_4/V_4$ is a group of order $6$ and there are two groups of order $6$, $S_3$ and $Z_6$.

But $S_4/V_4 \not \cong Z_6$ since $S_4$ has no elements of order $6$ or a multiple of $6\implies S_4/ V_4\cong S_3$.

mesel
  • 14,862