Why does $\sin(0)$ exist?

Question

I can't understand why should $\sin(0)$ exist, because if an angle is $0^{\circ}$, then the triangle doesn't exist i.e. there is no perpendicular or hypotenuse. However, if we take $\lim_{x \to 0} \sin(x)$, then I can understand $$\lim_{x \to 0} \sin(x) = 0$$ since perpendicular $\approx$ 0.
So although $\lim_{x \to 0} \sin(x)$ is $0$, I can't understand how $\sin(0)=0$, and if $\sin(0)$ is not defined, then why is graph of $\sin(x)$ continuous ?

Answer 1

Trigonometric functions $\sin, \cos,..$ are defined by the means of triangles first but they are generalised by defining them on unit circle and using negative numbers.

$\sin\left ({3\pi\over 2} \right )=-1$ but ratio of two length can not be $-1$. (I think it is more interesting for $\sin(x) $ to be negative rather than to be $0$, when we regard triangles)

But this happens almost every area of math.(the generalisation of functions, definitions...)

As an example think the expression $2^n$. It had been used for " $n$ times multiply by $2$".

$2^3=2\cdot 2\cdot 2=8$ but what is the meaning of $2^{1\over 2}$ or $2^{-1}$. Now we are using all of them indeed, $2^x$ is defined for all $x\in \mathbb R$.

I hope what I mean is clear.

Answer 2

There is no triangle with an angle of $3 \pi / 2$ or $2 \pi$, but we nevertheless define $\sin(3 \pi / 2) = -1$ and $\sin(2\pi) = 0$.

Essentially, we want to generalize the sine of an angle between $0$ and $\pi / 2$ to a sine of any angle. To do this we use the unit circle: $\sin$ is the $y$-coordinate and $\cos$ is the $x$-coordinate. This agrees with the original definition of $\sin$ on the interval $0$ to $\pi / 2$ using triangles.

Answer 3

Triangles may be a motivation for the trigonometric functions, but they are not actually defined based on triangles. There are many equivalent ways to define them, for example they are easily defined using a power series, which will have no problem with sin (0).

There are many uses that are unrelated to triangles: For example, 3D graphics where rotations are calculated using trigonometric functions: It would be absurd to define sine and cosine in a way that rotation by zero degrees needs special treatment or doesn't work. If you calculate where the end of the seconds digit of your watch is depending on time, it doesn't make sense to define the sine function so that the calculation doesn't work once or twice a minute. Then there are applications like FFT where sine and cosine are heavily used, without any geometry involved at all.

Answer 4

I don't see why you'd have to take $\lim_{x \to 0} \sin(x)$. I'd like to argue that every line segment is a (degenerate) triangle. So with the definition of $\text{sin} = \frac{\text{perpendicular}}{\text{hypotenuse}}$, we get $\sin(0) = \frac{0}{\text{hypotenuse}} = 0.$

Similar reasoning can be applied to $\sin{90^{\circ}}$, $\cos{0^{\circ}}$, $\cos{90^{\circ}}$ and so on.

Answer 5

If you use right triangles for defining the trigonometric functions, you can't immediately give a sense to $\sin 0$, $\cos0$, $\sin\frac{\pi}{2}$ or $\cos\frac{\pi}{2}$ (let's limit to angles in $[0,\frac{\pi}{2}]$, for the moment).

For acute triangles we know the law of cosines $$ a^2=b^2+c^2-2bc\cos\alpha $$ where $a$, $b$, $c$ are the side lengths and $\alpha$ is the angle opposed to $a$. This law reduces to Pythagoras' theorem if $\alpha$ is a right triangle, so it's natural to define $$ \cos\frac{\pi}{2}=0 $$ in order to extend the law of cosines also to that case. But for acute angles we already know that $$ \sin\left(\frac{\pi}{2}-\alpha\right)=\cos\alpha $$ so, if we want to preserve this identity we have to define $\sin0=\cos\frac{\pi}{2}=0$.

Similarly, the law of sines says $$ \frac{a}{\sin\alpha}=\frac{b}{\sin\beta}=\frac{c}{\sin\gamma}=2R $$ where $\beta$ is opposed to $b$, $\gamma$ is opposed to $c$ and $R$ is the radius of the circumscribed circle. If we want this holds also for a right triangle, we must set $\sin\frac{\pi}{2}=1$ and so also $\cos0=1$.

However, these considerations are superseded by a different definition of the trigonometric functions. Consider the circle with center at the origin and radius $1$ in an orthogonal Cartesian reference system. If we draw the ray forming the angle $\alpha$ with the positive $x$-axis, then, by definition, $\cos\alpha$ and $\sin\alpha$ are, respectively, the $x$-coordinate and the $y$-coordinate of the intersection between the ray and the circle.

With this definition, $\sin0=0$ and $\cos0=1$ are obvious.

Answer 6

It is a degenerate triangle with altitude $0$, and therefore $\sin(0)=0$. This is a bit troubling but in a way is not that different from the question why the number $0$ exists in the first place. In fact, it took many centuries to accept this "degenerate" number as a legitimate one. This happened only in the 19th century, which is remarkably recent. In fact the ancient Greeks did not even accept $1$ as a genuine number (and certainly not the negatives, another relatively recent innovation).

Answer 7

What is $\sin$? What is $\sin(57.94°)$? According to the idea to which OP refers$$\sin(57.94°):=\frac{MH'}{OM}=\frac{OH}{OM}\simeq \frac{8.5}{10}=0.85$$ 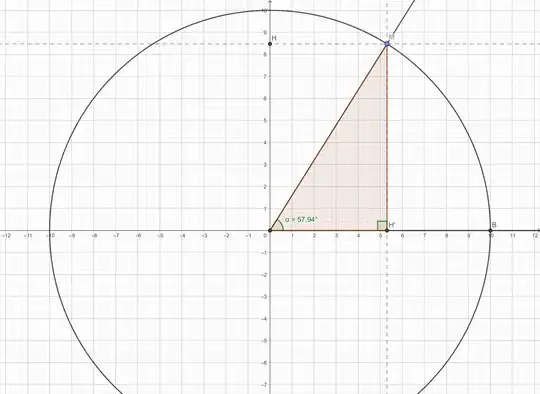But as the drawing suggests, his idea is just a restriction of more general ideas of what $\sin$ really is. For example, $$\sin(0)=0$$