1

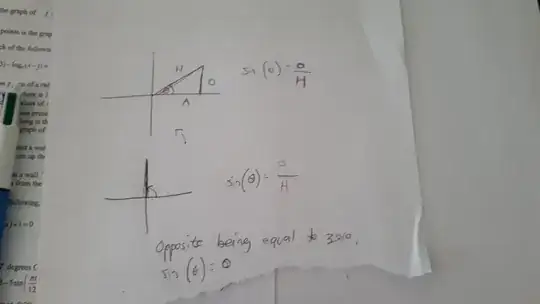
enter image description here

If o/h is = sin(90), wouldn't sin(90) = 0

Corey King
  • 41
  • 5
    As $\theta\to90^\circ$, opp and hyp both approach the same, so their ratio approaches $1$ – J. W. Tanner Dec 29 '20 at 00:22
  • 5
    Look at your picture, the green side (opposite) is the same length as the red (hypotenuse). – jlammy Dec 29 '20 at 00:22
  • 1
    Part of the difficulty might be that the triangle for $\theta=90^\circ$ is a degenerate triangle (the adjacent side has zero length), which is hard to visualize. There is also a problem at $\theta=0$ (https://math.stackexchange.com/q/794201/139123). And what if the angle is greater than $90$ degrees? You are starting to find out the limitations of using a triangle to define the trig functions. – David K Dec 29 '20 at 00:31
  • 1
    You should draw that picture with an 89 degree angle. – littleO Dec 29 '20 at 01:22

1 Answers1

2

As $\theta \to 90^\circ$, $\frac{O}{H} \to 1$. Because O and H become closer and closer to the same value. You can see that on your graph (just keep track of the colors, red and green are overlapping). Another way to look at it is by generalizing the trigonometric functions beyond side lengths of triangles. Once defined on the unit circle, by their Power Series (typically Taylor), or in terms of the complex exponential, the result is fairly trivial.

On the unit circle, that point is $y=1$ $(\sin = 1)$, $x=0$ $(\cos = 0)$.

By their Power Series, $\sin(\frac{\pi}{2}) = \frac{\pi}{2} - \frac{(\frac{\pi}{2})^3}{3!} + \frac{(\frac{\pi}{2})^5}{5!} - \frac{(\frac{\pi}{2})^7}{7!}...$, which you can see after the first few terms approaches $1$.

By the complex exponential, you have $\operatorname{Im} (e^{\frac{\pi i}{2}})$, which is $1$.

Ethan Bolker
  • 95,224
  • 7
  • 108
  • 199
Neptune
  • 420
  • 3
  • 11
  • 2
    The first three sentences here address the OP at their level of understanding. The remainder is (I think) too advanced, though correct. – Ethan Bolker Dec 29 '20 at 01:22