arctan equation question

Question

This question has two parts, I've done the first but I don't understand that second.

a. Show that $arctan(\frac{1}{2})+arctan(\frac{1}{3})=\frac{\pi}{4}$

b. Hence, or otherwise, find the value of $arctan(2)+arctan(3)$.

The mark scheme has a few methods to solve this, and I don't understand this one in particular.

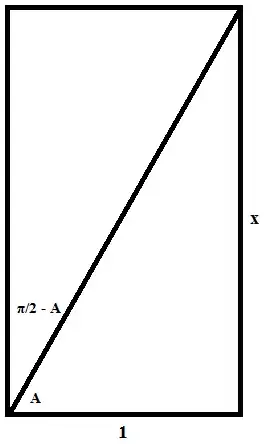
$**arctan(2)+arctan(3)=\frac{\pi}{2}-arctan(\frac{1}{2})+\frac{\pi}{2}-arctan(\frac{1}{3})**$

$=\pi-(arctan(\frac{1}{2})+arctan(\frac{1}{3}))$

$=\pi-\frac{\pi}{4}=\frac{3\pi}{4}$

I don't understand the line that I asterisked. Where does the $\frac{\pi}{2}$ and $arctan(\frac{1}{2})+arctan(\frac{1}{3})$ come from? Please could someone explain all of this to me?

Answer 1

We have for $x>0$: $$\arctan x+\arctan\left(\frac1x\right)=\frac\pi2$$ and to prove it: let $$f(x)=\arctan x+\arctan\left(\frac1x\right)$$ and by differentiate it we find $f'(x)=0$ so $f(x)=f(1)=\frac\pi2,\quad\forall x>0.$

Answer 2

hints:

Proof that

$$\arctan x=\frac\pi2+\arctan\frac1x\;,\;\;0<x\neq\begin{cases}\frac\pi2\\{}\\\frac2\pi\end{cases}+n\pi\;,\;\;n\in\Bbb Z\;\;:\;$$

$$f(x):=\arctan x+\arctan\frac1x\implies f'(x)=\frac1{1+x^2}-\frac1{x^2}\frac1{1+\frac1{x^2}}=0$$

and thus $\;f(x)=k=$ a constant. Now choose wisely some $\;x\;$ to find out what that constant is...

Answer 3

As $\displaystyle\tan\left(\frac\pi2-z\right)=\cot z,\arctan u+\text{arccot}u=\frac\pi2$

and use Are $\mathrm{arccot}(x)$ and $\arctan(1/x)$ the same function? or this, to show that $\displaystyle\arctan x=\text{arccot}\frac1x$ for $x>0$

See also : Proof of $\arctan{2} = \pi/2 -\arctan{1/2}$

Answer 4

$$arctg(a)+arcctg(a)=\pi/2$$ and $$tg(\alpha)=1/ctg(\alpha)$$

Answer 5

Sometimes drawing a diagram is helpful.

From the diagram it is clear that $$\tan A = x$$ $$A = \arctan(x)$$ and that also $$\tan(\pi/2 - A) = 1/x$$ $$\arctan(\tan(\pi/2 - A)) = \arctan(1/x)$$ $$\pi/2 - A = \arctan(1/x)$$ $$\pi/2 - \arctan(x) = \arctan(1/x)$$ or alternatively, $$\pi/2 - \arctan(1/x) = \arctan(x)$$