Find the axes of the ellipse

Question

What are the equations of the major and minor axes of the ellipse $x^2+2y^2-2xy-1=0$. The centre of the ellipse is $(0,0)$ but the axes are tilted (with respect to $x-y$ axes). I don't know how to find those.

Answer 1

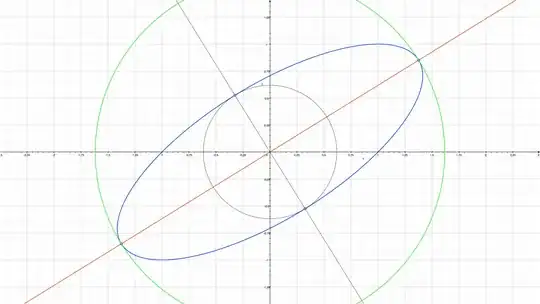First you should sketch a picture of your ellipse. The major axis lies along the line with equation: $ y = \frac{\sqrt{5} - 1}{2} x $

The minor axis will be perpendicular to the line of the major axis.

To find the length of the semi-major axis , find the distance between a point on intersection of the line above with the ellipse and the origin . Likewise the length of the semi-minor axis will be the distance between the point of intersection of the second line with the ellipse and the origin. I obtained this value by finding the maximum of x^2 + y^2 on the ellipse, ( this can be done in many ways, one is the method of lagrange multipliers.)

I'll include my sketch. You can take it down off the screen for a closer look. In regard to rotation of the axis, find the angle the red line makes with the x-axis , this will give you a good idea of what to try in terms of rotating your coordinate system.

Answer 2

You take an ellipse of the form $a x^2 + b y^2 + c x y + d x + e y + f = 0$ and match coefficients with the equation of an ellipse centered about $(x_c,y_c)$ at an oblique angle $\theta$

$$ \left( \frac{ (x-x_c) \cos\theta + (y-y_c) \sin\theta}{R_x} \right)^2 + \left( \frac{ -(x-x_c) \sin\theta + (y-y_c) \cos\theta}{R_y} \right)^2 - 1 = 0 $$

where $R_x$ and $R_y$ are the major and minor radii. From here we deduce that the coefficient $c$ is critical in defining the angle as you find that (by matching $x y$) $$ \sin(2 \theta) \left( \frac{1}{R_y^2} - \frac{1}{R_x^2} \right) + c = 0$$

You already have $(x_c,y_c) = (0,0)$ and $x^2+2 y^2 - 2 x y - 1 =0$ so I propose to change the coordinates to $$\begin{pmatrix} x \\ y \end{pmatrix} = \begin{bmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{bmatrix} \begin{pmatrix} x' \\ y' \end{pmatrix}$$ to get

$$ -(x'^2+4 x' y' - y'^2) \cos^2 \theta - 2 (x'^2 - x' y' -y'^2) \sin\theta \cos\theta + (2 x'^2 +2 x' y' + y'^2)-1 = 0$$

The correct choice of $\theta$ should convert the above to $\frac{x'^2}{R_x^2} + \frac{y'^2}{R_y^2}-1 =0$. If you match the $x' y'$ coefficients you get

$$ \left. 2 \cos(2 \theta) - \sin(2 \theta) = 0 \right\} \left. \tan( 2\theta) = 2 \right\} \theta = 31.71° $$

and

$$ R_x = \frac{\sqrt{5}}{2} + \frac{1}{2} = 1.618 \\ R_y = \frac{\sqrt{5}}{2} - \frac{1}{2} = 0.618 $$

_{Curious that these are equal to the golden ratio}