Proof $\;\frac{\sin x}{x} \xrightarrow[x\to 0]{}1$

Question

$$x < \tan x?$$

also, we assume that $x>0$, is this because we take the right hand limit?

There are many ways of doing so. Do you know Taylor expansion? — user88595, May 03 '14 at 14:26
@user88595 Yes, it does. The linked page is in Swedish. Also, "Sats" = "Proposition", more or less. — Arthur, May 03 '14 at 14:28
Please translate and rewrite the proof in the post if you want most people to be able to answer you. — user88595, May 03 '14 at 14:28
http://math.stackexchange.com/questions/98998/why-x-tanx-while-0x-frac-pi2 — Henrik Finsberg, May 03 '14 at 14:29
https://www.google.com/search?q=plot+x%2Ctan(x)&rlz=1C1JRYI_enIN487IN487&oq=plot+x%2Ctan(x)&aqs=chrome..69i57.8842j0j1&sourceid=chrome&es_sm=93&ie=UTF-8#q=plot+tan(x)%2Cx — evil999man, May 03 '14 at 14:32
In the link by Henrik, in the answer by David, it is completely clear from the geometrical figure why $;\sin x<\tan x;$ . — DonAntonio, May 03 '14 at 14:35
@Awesome A drawing of a graph is never a full proof. It can accompany and greatly help a proof, true, but it is not enough. If you rely too helvily on drawings, then you open up to intuition taking over where reasoning should be used, and you end up making mistakes, like in this proof that all triangles are isosceles. — Arthur, May 03 '14 at 14:37
The drawing in this case is so basic that it almost is a proof by itself. Anyway, doing a little trigonometry here and there the inequality follows at once. — DonAntonio, May 03 '14 at 14:39

evil999man · Answer 1 · 2014-05-03T14:59:35.790

1

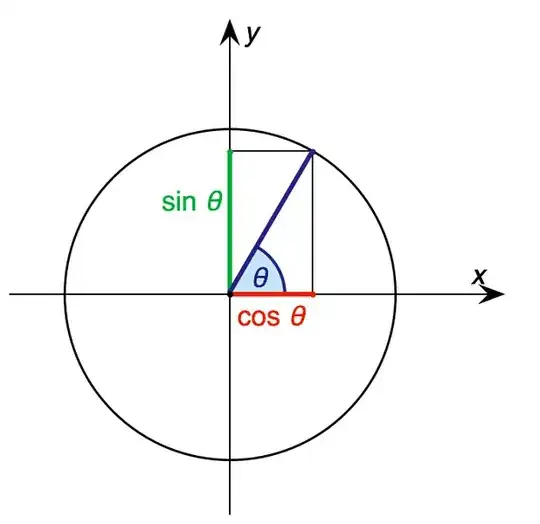
enter image description here

$$x=\frac{\text{arc}}{\text{radius}}$$

$$\sin{x}=\frac{\text{perpendicular}}{\text{radius}}$$

As $x\to 0,\text{arc}\to \text{perpendicular}$

Hence, $\lim_{x\to 0}\frac{\sin x}{x}= 0$

Now you can find derivatives of trigonometric functions and prove that derivative of $\tan x =\sec^2 x$

And then analyse the function $\tan x-x$ and see that it is non negative in $[0,\pi/2)$ and hence $x<\tan x$

Now you can proceed in your proof.

PS: I have a strange feeling that you might not want to go through the proof now.

edited May 03 '14 at 14:59

answered May 03 '14 at 14:39

evil999man

1

Well, one wants to prove that $\lim_{x\to0}\frac{\sin x}{x}=1$ in that way in order to compute the derivative of the sine function. So the derivative of the tangent is not available. – egreg May 03 '14 at 14:44
@egreg Edited... :P – evil999man May 03 '14 at 15:00
how come that "strange feeling" of yours? – jacob May 03 '14 at 20:50

1 Answers1