Can RUBIK's cube be solved using group theory?

Question

Can RUBIK's cube be solved using group theory? If yes, how can we use it to solve a $2\times2$ Rubiks Cube?

Answer 1

The difficult part of answering this question is to decide what it means to "use" group theory to solve the cube.

Clearly it is possible to learn to solve the cube without knowing any group theory, just by memorizing a procedure for doing so. And one can go a long way beyond rote memoization just by geometric/spatial intuition, again without any open appeal to group theory.

On the other hand, many people who solve cubes and do know group theory tend to think in group-theoretic terms while solving, or at least while refining their solving methods. Many well-known combinations can be analyzed as commutators or conjugations of elements in the cube group, which makes it easier to remember them and easier to understand why they work.

When it comes to being sure that one's solution method always works, I don't think there's any reasonable way around some group theory. For example, if you go look up a cookbook method for solving the cube, it doesn't tell you what to do if you end up in a state where the cube is solved except that two corner pieces need to be swapped. At best the cookbook method will assert that this situation cannot occur using legal moves -- but in order to convince yourself that this is true (except by the combined experience of a lot of experiments) you need some kind of proof. And this proof will either be based on the theory of permutation groups, or will effectively reinvent a part of this theory with different words.

---

I solve 2×2×2 cubes by imagining they are 3×3×3 and doing only those parts of my usual methods that take care of the corner pieces. Doubtlessly there are more efficient ways to go about it.

Answer 2

I cannot allow this question to go by without mentioning: Morwen Thistlewaite. This is a British mathematician who used group theory to find the smallest known bounds on how many face twists it takes to reach the solved state from an arbitrary state, along with some knowledge of which twists to take (a.k.a 'God's Algorithm'). Instead of positioning individual cubies in sequence, his is a more holistic approach called 'descent through nested sub-groups'. It works something like this:

A) Begin with the whole Cube group: G.

B) Pick a set of face twists generating a proper sub-group: H [example: the sub-group generated by twisting faces L, R, F, B, but NOT U, D]. For best results pick H such that |G|/|H| is as small as possible.

C) For each coset of H, find the shortest sequence of twists which will transform any member of the coset to a member of the sub-group [each coset is of the form aH; if b is in aH, then bH=aH; find the element b in aH generated by the fewest twists, and take the twist sequence for the inverse of b].

D) If H=E (i.e H is the trivial sub-group), stop. Otherwise replace G with H and return to (B).

To solve a scrambled Cube with this approach, one must determine which coset of the top-most sub-group contains the Cube's starting state, and make the sequence of face-twists calculated in (C) for that coset; this will change the cube to a scrambled state within the top-most sub-group. Repeat for each successive nested sub-group until you reach E; at that point the Cube has been unscrambled.

With this approach Thistlewaite was able initially to show that unscrambling any scrambled state takes no more than 26 (?) twists [source: 'Metamagical Themas' by Hofstadter, in Scientific American (I forget which exact issue)]. Since then he has been able to reduce this number enough to determine the theoretical maximum number of twists required.

Answer 3

[This is just about how commutators and conjugates help with rote memorization. I am yet to understand how the moves were designed]

Ref: https://momath.org/wp-content/uploads/2019/03/How-to-Solve-the-Rubiks-Cube_-All-6-Sides.pdf

For group ${ G }$ and ${ a,b \in G }$ we have commutators ${ [a,b] = aba^{-1}b^{-1} }$ and conjugates ${ a b a ^{-1} }.$

In the context of above document:

In short the main steps are:

• White corners: Repeat ${ [R ^{-1}, D ^{-1}] }$
• Middle layer: ${ [U, R] [U ^{-1}, F ^{-1}] }$ and ${ [U ^{-1}, L ^{-1}][U, F] }$
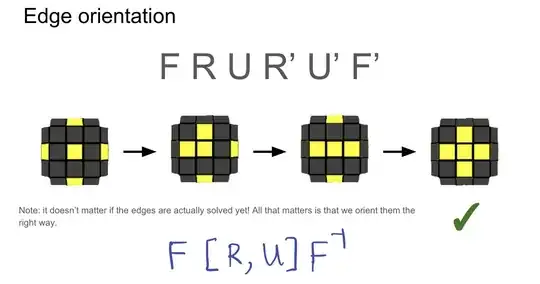
• Yellow edge pieces: ${ F [R, U] F ^{-1} }$ till yellow cross, then ${ (RU) [R ^{-1}, U] (RU) ^{-1} }$ till yellow edges align
• Yellow corner permutation: Repeat ${ [U R U ^{-1}, L ^{-1}] }$
• Yellow corner twisting: Effectively like white corners

---

Edit: Page 4 of Daniel Bump's notes here explains the importance of commutators, and how for example ${ [U R U ^{-1}, L ^{-1}] }$ moves very few pieces in the cube. (Intuitively, because the supports of ${ U R U ^{-1} }$ and ${ L ^{-1} }$ overlap very little). The full course page is here.