Can you give me some concrete examples of magmas?

Question

I've seen the following (e.g. here):

I've learned a bit about groups and I could give examples of groups, but when reading the given table, I couldn't imagine of what a magma would be. It has no associativity, no identity, no divisibility and no commutativity. I can't imagine what such a thing would be. Can you give a concrete example of a magma?

Answer 1

A ("strict") magma you've probably heard of is the vector cross-product in $\Bbb R^3$: $$ (a, b, c)\times(x, y, z) = (bz - cy, cx - az, ay - bx) $$ $\Bbb R^3$ is closed under this operation, but it has neither associativity, commutativity, identity nor divisibility.

Kind of in the same way that any square, any rectangle and any parallelogram fulfills the criteria of a trapezoid, and thus are trapezoids, we say that any group, monoid or semigroup is also a magma. All we demand from the structure in order to call it a magma is that it is closed under the binary operation.

And just as any trapezoid in which all angles happens to be right still is a trapezoid even though most people would call it a rectangle, so too will any closed / total algebraic structure with associativity, identity and divisibility be a magma, even though most people would call it a group.

Answer 2

A magma is just a set $X$ together with a binary operation on $X$, i.e. a function $X\times X\to X$. Any such function will do!

For example, we could define a binary operation on $X=\mathbb R$ by

$$x\cdot y = xy+x^2-y.$$

Answer 3

My favorite example: the operation $*$ on the odd integers with $a * b = (3a + b) / 2^k$ where $2^k$ is the highest power of $2$ dividing $3a + b$. With this notation, the Collatz conjecture can be restated:

For all odd integers $k$, does there exists an $n$ such that $$ \underbrace{\Big(\big(((k * 1) * 1) * \cdots \big) * 1\Big) * 1}_{n \text{ ones}} = 1? $$

Perhaps this sheds little light on actually solving the problem, but at least it provides a framework where the conjecture makes sense. The unpredictable, nonassociative behavior of this operation $*$ is one way of understanding why the Collatz problem is so hard.

Answer 4

As other people have pointed before you should pay attention to definition of magmas: it doesn't require that operation satisfies any property (associativity, existance of identity,etc) but it doesn't require either that the operations have to satisfy non associativity or non identity properties.

Anyway here's an example of magma which doesn't satisfy associativity (nor existance of identity).

Let $X$ be the set of finite planar binary trees. Given two trees $a$ and $b$ then we can form the tree $a \cdot b$ obtained from the union of the two trees adding a new root.

This operation is well illustrated by the following images: it should take two trees such as

and return a tree such as the following one

This is of course a binary operation and non associativity can be proven by drawing some trees. Non existance of identity follow from the fact that whatever trees you compose via this operation the composed tree has a depth strictly greater than both input trees.

Hope this helps.

Answer 5

The Cayley table $$\begin{array}{c|ccc} \ast & 0 & 1 & 2 \\ \hline 0 & 0 & 2 & 0 \\ 1 & 1 & 0 & 0 \\ 2 & 0 & 0 & 2 \end{array}$$ represents a finite groupoid or magma of order $3$ over the set $\{0,1,2\}$. It is not commutative, nor associative; it has no cancellation (left nor right), hence no division; it has no identity. Light years far from a nice group.

This book contains a lot of further examples of Cayley tables of finite groupoids: as you know, an operation (function) $\ast$ may be well defined both by an expression such as

$$a\ast b:=a+2b$$

or by the (finite) table with the whole set of values.

If you are looking forward examples of bare groupoids, it may be worth to dedicate some attention to finite structures in particular.

---

The set $\mathbb{R}^+$ of positive real numbers with exponentiation operation $a^b$ is an example of "strict" non-finite groupoid used by R.H. Bruck in his paper What is a loop? (1963).

---

Other examples of magmas over $\mathbb{Z}$ and $\mathbb{C}$ which are not semigroups nor quasigroups are included in this article (On congruences of groupoids closely connected with quasigroups) by Shcherbacov, Tabarov, Puscasu (2009). You should better look for a free two-page preview of it.

Answer 6

I wonder if an operation that returns the winning shape of the game Rock Paper Scissors isn't an example of a Magma, but none of the other structures...(?)

I'm a programmer, not a mathematician, so perhaps I'm totally misunderstanding the entire concept, but in Haskell, I would define the domain as

data Shape = Rock | Paper | Scissors deriving (Eq, Show)

I hope this is sufficiently self-explanatory for non-programmers, but this declares a type (a set, in this case) that contains three (and only three) elements, Rock, Paper, and Scissors. (Don't worry too much about Eq and Show - Eq enables us to compare two of these values with each other, and Show enables our command-line interface to print a representation of a value.)

We can now define an operation <> which returns the winner of two shapes:

(<>) :: Shape -> Shape -> Shape
Rock     <> Rock     = Rock
Rock     <> Paper    = Paper
Rock     <> Scissors = Rock
Paper    <> Paper    = Paper
Paper    <> Scissors = Scissors
Paper    <> Rock     = Paper
Scissors <> Scissors = Scissors
Scissors <> Rock     = Rock
Scissors <> Paper    = Scissors

Again, I hope this is readable even for non-programmers. The top line (<>) :: Shape -> Shape -> Shape simply declares that <> is an operation that takes two Shape values and returns a Shape value. Thus, it's a binary operation that closes over Shape (if I got my terminology right).

You can read this function implementation as a table. For example, if you have a Paper and a Scissors value, you find the Paper <> Scissors entry in the table, the result of which is Scissors.

This operation is certainly not associative:

*RPS> (Paper <> Rock) <> Scissors
Scissors
*RPS> Paper <> (Rock <> Scissors)
Paper

I don't know how to prove that no identity element exists, but I don't think it does.

If I correctly understand the invertibility requirement of quasigroups correctly, I don't think the operation is invertible. According to Wikipedia, for each a and b, there exist unique elements x and y such that both

a <> x = b,
y <> a = b

hold. However, if we set a = Rock and b = Scissors, there's no x or y that fulfill

Rock <> x = Scissors,
y <> Rock = Scissors

so I don't think this is a quasigroup either...

Answer 7

One magma that I like is a magma with operation C:{0, 1}$\rightarrow${0, 1} described by this table:

C  0  1
0  1  1
1  0  1

It's not commutative, associative, it doesn't have an identity, and has no divisor (if there is no identity, there cannot exist a divisor). Interestingly, for this magma if C(p, q)=1, as well as p=1, then q=1.

With that in mind, more interestingly, for this magma,

$\forall$ p $\forall$ q $\forall$ r $\forall$ s [C ( C ( C (p, q), r), C ( C (r, p), C(s, p)))=1].

Answer 8

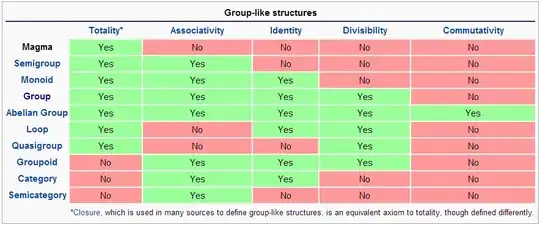
Here's another example, I think, with the admonition that I'm a programmer, not a mathematician. Even so, I was just now researching various operations in relationship to group-like structures, and came about the following example.

Mixing colours

It relates to mixing colours using Red Green Blue (RGB) colours. These are, for example, used in HTML pages.

As in my other example here on the page, I'm going to give my example in Haskell, but I'll try to provide enough information that non-programmers should be able to get the gist of it.

We can define the entire domain (set of possible values) as a data type called RGBColor:

data RGBColor = RGBColor { red :: Byte, green :: Byte, blue :: Byte }

This simply states that an RGBColor value has three constituent Byte (8-bit) values for the colours red, green, and blue. The lower the number, the darker the colour, and vice versa. Here's a single example that renders a yellow colour:

RGBColor 255 255 0

If you have two colours, you can mix them by taking half of the red component from each, half of the green component from each, and so on.

If we have, e.g.

λ> let x = RGBColor 100   0 128
λ> let y = RGBColor 200 255  64

we can mix these two RGBColor values (x and y) with a mix function:

λ> x `mix` y
RGBColor {red = 150, green = 128, blue = 96}

This returns a new RGBColor value with a mix of the two input colours. The mix function is a binary operation that takes two RGBColor values and returns an RGBColor value. Therefore, if I've understood just a minimum of all this, it must be at least a magma. Is it anything else? I don't think it is.

Associativity

Is the mix operation associative? No, it isn't, because it's easy to come up with a counter-example:

λ> (RGBColor 67 108 13 `mix` RGBColor 33 114 130) `mix` RGBColor 38 104 245
RGBColor {red = 44, green = 108, blue = 158}
λ> RGBColor 67 108 13 `mix` (RGBColor 33 114 130 `mix` RGBColor 38 104 245)
RGBColor {red = 52, green = 108, blue = 100}

Depending on where you put the brackets, the result is different, where it should have been the same.

Identity

Does an identity element exist for the mix operation? Here, we can use a combination of brute force and a counter-example to show that no identity element exists.

Let's arbitrarily pick a near-black colour to start with:

λ> let nearBlack = RGBColor 1 1 1

The reason I didn't pick absolute black (RGBColor 0 0 0) is that, due to rounding when mixing, there are eight candidates for absolute black. As we shall see, there's only one candidate for nearBlack:

λ> filter (\e -> e `mix` nearBlack == nearBlack) allColors
[RGBColor {red = 1, green = 1, blue = 1}]

This expression searches through allColors for a value, e, that behaves like the left identity for nearBlack. Here, allColors is an enumeration of all 16,777,216 possible RGBColor values - yes: it takes a couple of minutes to run the above search, but nothing more than that...

The point here is that if there's a left identity for mix, it must be RGBColor 1 1 1, because that's the only possible candidate for nearBlack. It holds for nearBlack:

λ> RGBColor 1 1 1 `mix` nearBlack
RGBColor {red = 1, green = 1, blue = 1}
λ> nearBlack == it
True

The return value (implicitly called it) is, indeed, equal to nearBlack. Can we find a counter-example where the candidate color does not behaves like the left identity?

Yes, easily:

λ> RGBColor 1 1 1 `mix` RGBColor 3 3 3
RGBColor {red = 2, green = 2, blue = 2}
λ> RGBColor 3 3 3 == it
False

The candidate RGBColor 1 1 1 does not behave as the left identity for the colour RGBColor 3 3 3, but it was the only candidate we had. Therefore, there's no identity element for the mix operation.

Invertibility

Is the mix operation invertible? No. We can demonstrate that with another combination of a counter-example and brute force. Pick these two values:

λ> let a = RGBColor  94  35 172
λ> let b = RGBColor 151 185   7

These will serve as the a and b in the definition of invertibility. Here, I'm using the definition from Wikipedia's article on quasigroups, because that's the only remaining type of operation that mix can be, now that I have demonstrated that it's neither associative nor has identity.

For every a and b, there must exist an x and y such that:

a `mix` x = b,
y `mix` a = b

First, try to find x for the above a and b:

λ> any (\x -> a `mix` x == b) allColors
False

The built-in any function returns True if there's any value in allColors that satisfy the lambda expression in the middle. The answer is False, so there's no need to continue. The above a and b serve as a counter-example, because there's no x that satisfy left division.

Summary

Mixing of RGB colours seems to be a magma, but no other type of operation. It doesn't have associativity, an identity element, and nor is it invertible.

---

Appendix

For programmers, here's the full code listing:

module RGB where

import Data.Bits ((.&.))
import Data.Word (Word8)
import Text.Printf (printf, PrintfType)

type Byte = Word8
data RGBColor = RGBColor { red :: Byte, green :: Byte, blue :: Byte }
                deriving (Eq, Show, Bounded)

instance Enum RGBColor where
  toEnum i = RGBColor r g b
    where
      r = toEnum $ (i .&. 0xFF0000) `div` 0x10000
      g = toEnum $ (i .&.   0xFF00) `div` 0x100
      b = toEnum $  i .&.     0xFF
  fromEnum x =
    fromEnum (red x) * 256 * 256 + fromEnum (green x) * 256 + fromEnum (blue x)

mix :: RGBColor -> RGBColor -> RGBColor
mix x y = RGBColor newRed newGreen newBlue
  where
    newRed   = round $ (toRational (  red x) + toRational (  red y)) / 2
    newGreen = round $ (toRational (green x) + toRational (green y)) / 2
    newBlue  = round $ (toRational ( blue x) + toRational ( blue y)) / 2

toWebColor :: PrintfType t => RGBColor -> t
toWebColor (RGBColor r g b) = printf "#%02X%02X%02X" r g b

allColors :: [RGBColor]
allColors = [minBound .. maxBound]

Answer 9

Here's a fun magma: function types $A \rightarrow B$ (handwaving dependent types/cumulative hierarchy).

It's Total

$(\rightarrow) : \textrm{Type}\rightarrow' \textrm{Type} \rightarrow' \textrm{Type}$

Not Commutative

$\textrm{Unit}\rightarrow\bot\cong\bot\;$, because there exists no proof (think $T\rightarrow F\equiv F$, or $0^1=0$).

$\bot\rightarrow\textrm{Unit}\cong\textrm{Unit}\;$, there's one proof by function-extensionality (think $F\rightarrow T\equiv T$, or $1^0=1$).

Not Associative

$\textrm{Bool}\rightarrow(\textrm{Unit}\rightarrow\textrm{Bool})\cong\textrm{Bool}\rightarrow\textrm{Bool}\;$, there are only four such functions.

$(\textrm{Bool}\rightarrow\textrm{Unit})\rightarrow\textrm{Bool}\cong\textrm{Unit}\rightarrow\textrm{Bool}\;$, of which there are two, just return a constant.

Only a Left Identity

$\forall A:\textrm{Type}.(\textrm{Unit}\rightarrow A\cong A)\;$, again we ignore the argument and return a constant.

I haven't thought too hard on invertibility, which would require a little more insight on the algebra of types.