5

Why does the integral of the surface area of a sphere equal it's volume?

$$\int{4\pi r^2 \ \mathrm{d}r =\frac{4}{3}\pi r^3}$$

I don't quite understand why the relationship between surface area and volume is this way. Is this true for any other shapes?

Bennett Gardiner
  • 4,163
codedude
  • 807
  • 3
    True for circles as well. Area = $\pi r^2$. Circumference = $2\pi r$. So here's the question: does it hold for all $n$-spheres? Other kinds of surfaces? – Kaj Hansen May 02 '14 at 05:27
  • Integrating the surface equation gives you the volume that the surface encloses like when you integrate the function of a graph you obtain the area under the curve. – Kal S. May 02 '14 at 05:30
  • So would this apply to say a square-because integrating 6x^2 doesn't give me x^3 – codedude May 02 '14 at 05:31
  • I'm sorry... I meant a cube. Clearly it's too late for math. :) – codedude May 02 '14 at 05:40
  • 1
    If you consider the radius of a cube to be the distance $r$ from center to middle of a face, then its volume is $(2r)^3$ and its surface area is $6(2r)^2$. Integrate from $r=0$ to $r=r$. – DanielV May 02 '14 at 05:42

2 Answers2

4

The reason is essentially the same as the reason why the volume of an onion is the same as the volume of all its layers. Imagine a spherical ball as being composed of many thin spherical layers, like an onion. The volume of the layer between radius $r$ and radius $r+\delta r$ is (to a close approximation if $\delta r$ is small enough) the area $4\pi r^2$ times its thickness: $4\pi r^2\cdot\delta r$. Summing all these small volumes from the centre of the ball ($r=0$) to its outer radius ($r=a$, say) and taking the limit as the $\delta r$ tend to $0$ gives us the limit $$\int_0^a 4\pi r^2\mathrm dr.$$As you know, this evaluates to $\frac43\!\pi a^3$, the volume of the sphere.

John Bentin
  • 18,454
3

I'm sure some will have an issue with the technical aspects of the following explanation, but I believe that it should intuitively help.

One way to think about the area under a curve (and the definite integral), is to picture a vertical line from the horizontal axis to the graph of your function. Starting at say $x=0$, picture this line moving to the right. As it does, and its height changes, it will touch along the way a set of points in the plane (shaded below). Perhaps think about this line as being covered in paint, and as it moves along it paints the area under the curve. 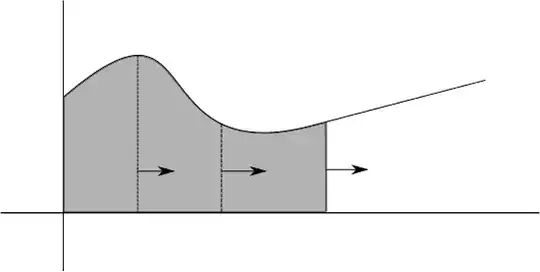enter image description here

You can view the definite integral $$\int_0^xf(t)dt$$ as suggesting the motion of this line of changing height on the horizontal axis from 0 to $x$ and giving you the area of the region that it "paints".

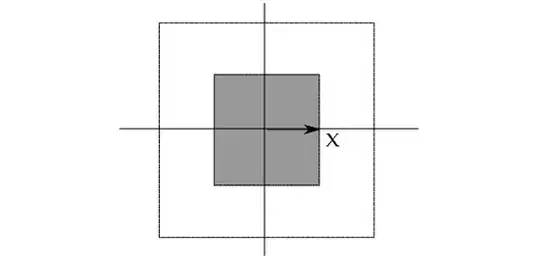
The same thought process works for other shapes. Consider a square centered at the origin. enter image description here

The perimeter of this square is $8x$. Think of $x$ starting at zero and increasing. As the square increases in size, its perimeter will also "paint" a collection of points in the plane, and we can think about the area of the square as being the painted points. In the same vein as above, the integral $$\int_0^x8tdt=4x^2$$ suggests the painting of these points and gives us the area of the resulting collection of painted points (you can easily see that $4x^2$ is the area of the shaded square).

Likewise for a circle when integrating the circumference gives the area: $$\int_0^r2\pi tdt=\pi r^2$$

Three dimensional shapes are a little harder to picture (and definitely harder to draw), but you can think about them in the same way. Extending the square example to a cube, we can now think about the faces of the cube (its surface area) as "painting" a volume of points. Consider a cube centered at the origin, with the horizontal axis going through the center of opposing faces. The surface area of such a cube is $24t^2$ (check) when it has "radius" $t$. Integrating $$\int_0^x24t^2dt=8x^3$$ gives the volume of points touched by the faces of the cube as it expands from radius 0 to radius $x$.

Hopefully, by using the same sort of thought process on a sphere, you'll find that it makes a little more intuitive sense that the integral of its surface area gives us its volume.

Scott H.
  • 558