19

I was reminded by question 77569 about something that has bothered me off and on for a while now. Consider the model of the projective plane given by the last diagram on page 37 of these notes (it's just a lens-shape in the plane, with opposite sides identified in a "chasing" way):

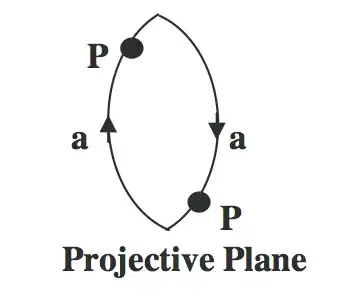
Möbius strip

Now if you remove an open disk from it, what's left, call it $M$, is homeomorphic to a Möbius strip. Unlike the projective plane, the Möbius strip can be embedded in ${\bf R}^3$ with no self-intersections. So it's natural to ask whether you can use the model $M$ to construct a physical Möbius strip. That is, does the presence of the hole make it possible to carry out in 3-space the indicated identification of edges, without tearing or self-intersection, provided the material being used is sufficiently elastic.

Experiments with paper have not been encouraging. Is there some obstruction to making a Möbius strip from $M$?

Another plane model for a Möbius strip is a triangle with 2 edges identified "chasing" and one edge unidentified. The 2nd figure on page 40 of those notes will do as an illustration. Again, I haven't been able to carry out the identification with paper in 3-space; is it possible? or is there some obstruction?

I should add that of course I know that one can make a Möbius strip from the usual model, a rectangle with one pair of opposite edges identified chasing. And I know that these other models are homeomorphic to the Möbius strip. The questions are about using the other models to make a Möbius strip.

Community
  • 1
Gerry Myerson
  • 179,216
  • As for your second example of a triangle, that is very close to the usual rectangle model. If you have a trapezoid with two opposite sides of length $1$ and $\epsilon$ unidentified, and the other two opposite sides identified with the "chasing" orientation, then the the triangle model is the limit as $\epsilon\to 0$. The usual strip model happens when $\epsilon=1$. – Cheerful Parsnip Nov 01 '11 at 01:04
  • That seems to be a strange direction to go in -- since the model in the notes is not an actual embedding into $\mathbb R^3$ (they say "we’re not too worried about where these surfaces live, we won’t pursue that point"), you couldn't construct it to start with and cut out a disk from it. I suppose you could remove one of the "eardrums" from a Boy's surface and get a partially self-intersecting Möbius strip, though. – hmakholm left over Monica Nov 01 '11 at 01:07
  • @Jim, yes, and now I am reminded that I think I saw a discussion somewhere of how short the unidentified sides of a rectangle could be (relative to the identified pair) and still permit making a Mobius strip. I'll have to see if I can find it. But are you suggesting your comment answers my question? – Gerry Myerson Nov 01 '11 at 01:12
  • @Henning, we have a failure of commutativity here. I didn't mean, construct the projective plane, then cut out a disk; I meant, cut out a disk (from the diagram), then construct a Mobius strip (if possible). – Gerry Myerson Nov 01 '11 at 01:15
  • @t.b., thanks for the edit. – Gerry Myerson Nov 01 '11 at 01:15
  • @GerryMyerson: No I'm just observing. I also tried making a model of the first one (lens minus disk) out of paper and tape, and I couldn't get it to glue up. – Cheerful Parsnip Nov 01 '11 at 01:16
  • @GerryMyerson: Have you seen Stephen Barr's book "Experiments in topology." I can view it on Google books. Chapter 3 is about constructing the "shortest Möbius strip." – Cheerful Parsnip Nov 01 '11 at 16:40
  • @Jim, yes, I realized yesterday that that was where I had seen the discussion I referred to in my earlier comment. I believe Barr completely solves the problem of the triangle model. If I get some time today to read it and digest it I may post a summary as an answer. Together with Henning's answer to the other part of my question (once I've understood it), that should settle matters. – Gerry Myerson Nov 01 '11 at 21:38

2 Answers2

7

Note that if you cut a disk out of your lens shape, the remaining annulus is embedded in $\mathbb{R}^3$ without any "twists". If this could be "glued" to itself to form a Möbius band in $\mathbb{R}^3$, then the (external) boundary of your lens-shape region would be mapped to the "soul" of the Möbius band; namely, the curve running along the middle of the Möbius band for one of the standard embeddings.

However, it is easy to check that if one cuts the Möbius band open along its "soul", one gets a strip with two twists as you make full circle around it, rather than the strip with no twists that would result if one removed a disk from the "lens". Thus such a construction is impossible. Note that the use of the term "soul" is consistent with the term used in Riemannian geometry for manifolds of nonnegative curvature.

azimut
  • 22,696
Mikhail Katz
  • 42,112
  • 3
  • 66
  • 131
6

You could cut out a very large disk so only a small (half-)strip along the edge of the diagram is left. You then get the problem that this punctured but flat diagram is not twisted in the right amount to be glued together along the edge into a physical Möbius strip.

Alternatively, however, cut out a disk that spans the edge of the diagram. What is left is now ready to be twisted and glued together in the completely standard construction of a Möbius strip. That's not much extra fun, of course.

Community
  • 1
hmakholm left over Monica
  • 286,031